Lug Analysis
A lug, also known as a lifting lug or a padeye, is essentially a plate with a hole in it where the hole is sized to fit a clevis pin. Lugs are used in combination with clevis pins to transmit load between different mechanical components. Common applications where lugs are used include:
- strongbacks with padeyes, lifted with shackles and other rigging
- connections between actuators and other structure (i.e. trunnion joint, clevis joint)
- door hinges
Advantages of lugs over other types of connections that are used to transmit load include:
- rotation between components is possible
- quick and simple installation
Contents
Lug Analysis Overview
Analysis of a lug is deceptively complex since there are several simultaneous, interacting failure modes. These failure modes are associated with different areas of the lug, as illustrated in the figure below (Note: Figure not to scale):
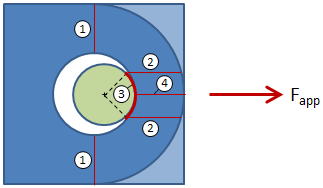
The failure modes for the lug are listed below. The numbers correspond with the labeled sections from the above figure:
- Tension failure across the net section
- Shear failure along two planes
- Bearing failure
- Hoop tension failure / fracture on single plane
- Out of plane buckling ("dishing") -- (not shown in the figure)
There are several common methods of analyzing a lug:
- Simplified analysis - This method is based on first principles and involves making simplifying assumptions about the nature of the failure and calculating factors of safety. This has the advantage of being relatively easy, but it only gives an approximate determination of the adequacy of the lug.
- Air Force Method - This method considers most of the failure modes above, and it uses empirical curves to determine more accurate allowable loads. This method allows for lugs under axial loading, transverse loading, or oblique loading. This method also accounts for the interaction between the lug and the clevis pin.
- ASME BTH - This method considers most of the failure modes above, and it uses simplified equations with correction factors based on empirical data to determine more accurate allowable loads. This method is simpler than the Air Force Method, but it only allows for lugs under axial loading and does not account for the interaction between the lug and the clevis pin.
All of these methods are described in the following sections.
Simplified Analysis
This method is based on first principles (as well as on the simplified method outlined in Bruhn) and involves making simplifying assumptions about the nature of the failure. While it is relatively easy to perform, it only gives an approximate determination of the adequacy of the lug and should not be employed for critical structure.
In the simplified analysis, the following failure modes are considered:
- Tension failure across the net section
- Shear failure along two planes
- Bearing failure
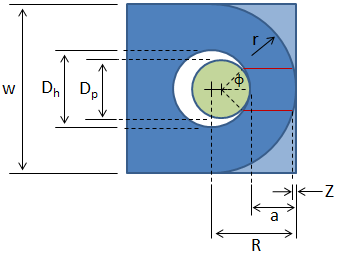
A factor of safety is calculated for each of the failure modes, and as long as each factor of safety is acceptable then the lug can be considered to pass. The figure below shows the lug in blue and the pin in green.
The dimensions in the figure are:
- Dh = hole diameter
- Dp = pin diameter
- R = edge distance (distance from center of hole to edge of lug in direction of applied load)
- r = radius of curvature of edge of lug (greater than or equal to R)
- a = distance from edge of hole to edge of lug = R − 0.5 Dh
- w = width
- t = thickness (not shown in figure -- thickness is into the page)
- Z = loss in shear plane length due to curvature at end of lug
- ϕ = shear plane locating angle = 40°
Need a Lug Calculator?
Try our lug calculator based on the methodology described here.
- Allows for axial, transverse, or oblique loading
- Performs calculations for lug strength, pin strength, and double shear joint strength
Tension Failure Across Net Section
Tension failure across the net section occurs over the cross-section highlighted in red in the figure below:
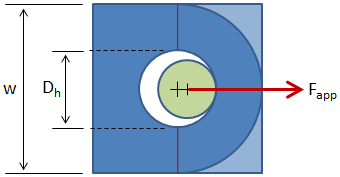
The area of the net section is given by:
The ultimate tensile load is the load that would result in tensile failure across the net section, and is given by:
where Stu is the ultimate tensile strength of the lug material. The equation above assumes a uniform tensile stress over the cross-section. In reality there will be a stress concentration due to the flow of stress around the hole.
The factor of safety is given by:
Shear Tear Out Along Two Planes
Shear tear out occurs over the two shear planes highlighted in red in the figure below:
The total shear plane area is given by:
where Lsp is the length of the shear plane and t is the lug thickness. A simple and conservative approach is to calculate the length of a single shear plane as:
where a = R − 0.5 Dh, as shown in the figure above. If it is desired to account for a slightly longer shear plane, it is common practice to consider a 40 degree line extending from the center of the shear pin. At the point where that 40 degree line intersects the pin hole, extend the shear plane horizontally to the outer edge of the lug. In this case, Lsp is calculated as:
where ϕ is the shear plane locating angle of 40° and Z is the loss in shear plane length due to the curvature at the end of the lug. This loss is calculated as:
Note that if the lug end is flat then r is infinity and Z is zero.
The ultimate shear load is the load that would result in shear tear out along the two planes, and is given by:
where Ssu is the ultimate shear strength of the lug material.
The factor of safety is given by:
Bearing Failure
Bearing occurs between the surface of the pin and the inner surface of the hole in the lug, as shown in the figure below:
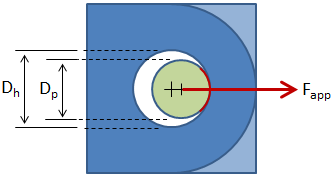
The bearing area is given by:
Note that since the length of the bearing surface is equal to the diameter of the pin, and since the circumference of a circle is given by C = πD, then:
- the length of the bearing surface is also equal to 1/π times the circumference of the pin
- the swept angle of the bearing surface is equal to 2 radians ≈ 115°
The ultimate bearing load is the load that would result in bearing failure, and is given by:
where Sbru is the minimum of the ultimate bearing strength of the lug material and the ultimate bearing strength of the pin material. The ultimate bearing strength can be approximated as 1.5·Stu.
The factor of safety is given by:
If a bushing is pressed into the lug, then bearing needs to be calculated for both sets of contact:
- Pin on bushing
- Bushing on lug
Air Force Method
The Air Force Method of lug analysis is widely used in industry and is documented in the Stress Analysis Manual of the Air Force Flight Dynamics Laboratory (FDL). This method follows closely with the methods presented in Melcon & Hoblit and Bruhn, and it relies heavily on curves generated by empirical data. Although this method is somewhat more complex than other lug analysis methods, it is incredibly useful because it allows for lugs under axial loading, transverse loading, or oblique loading, and because it accounts for the interaction between the lug and the pin.
Check out our lug calculator based on the Air Force Method described here.
This section discusses axial loading, transverse loading, and oblique loading separately. These sections disregard the effect of the pin on the lug strength. A discussion of the pin and lug interaction is given at the end.
Axial Loading
For axially loaded lugs, the Air Force method evaluates the lug for bearing failure, shear-out failure, hoop tension failure, and failure across the net section. Three of the failure modes are actually combined into a single failure mode -- the "bearing strength" accounts for bearing, shear-out, and hoop tension. This is consistent with Bruhn and Melcon & Hoblit.
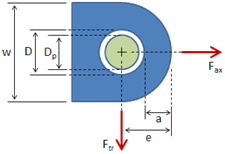
The dimensions of interest for an axially loaded lug are shown in the figure below:
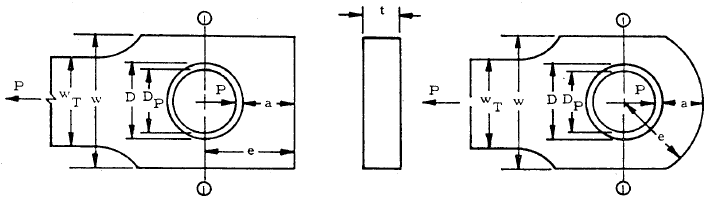
The dimensions from the figure include:
- D = hole diameter
- Dp = pin diameter
- e = edge distance
- a = distance from edge of hole to edge of lug = e − 0.5 D
- w = width
- t = thickness
Bearing Strength Under Axial Load
The ultimate bearing load, accounting for bearing, shear-out, and hoop tension, is given by:
where D is the hole diameter, t is the lug thickness, and Stu and Sty are the lug material's ultimate and yield tensile strengths, respectively. Fbru.L and Fbry.L are the lug ultimate and yield bearing stresses, respectively, and are given by the following equations:
| e/D < 1.5 | e/D ≥ 1.5 | |
|---|---|---|
| Ultimate Bearing Stress, Fbru.L: |
|
K Stu |
| Yield Bearing Stress, Fbry.L: |
|
K Sty |
For ratios of e/D less than 1.5, the hole is close to the edge of the lug and so shear-out and hoop tension are likely to be the most critical failure modes. For larger values of e/D, the hole is spaced farther from the edge and so bearing is likely to be the critical failure mode.
The factor K in the equations above is the allowable axial load coefficient which accounts for the interaction effects between the different failure modes (bearing, shear-out, and hoop tension). The value of K is read off of one of the following two plots. The first plot is used for D/t ≤ 5, which is the most common case. If D/t > 5 then the lug is thin, and in that case the value of K is read off of the second plot below. (Note 2)
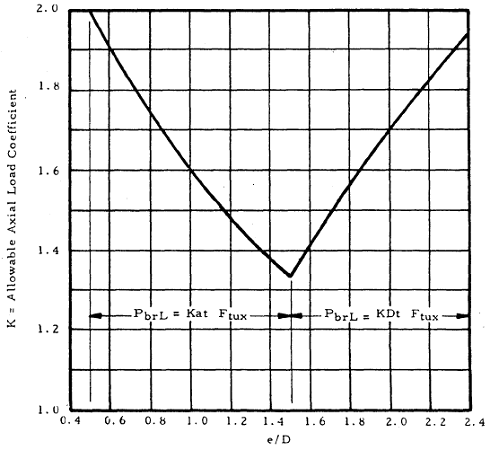
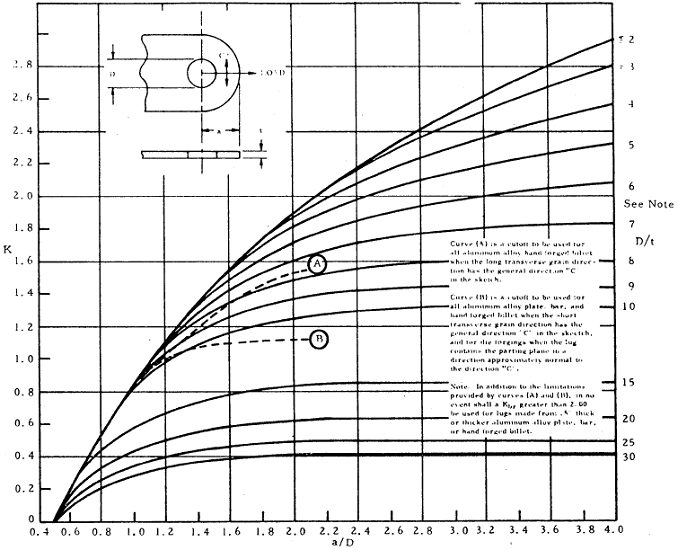
Bushing Bearing Strength Under Axial Load
If there is a bushing in the lug, then the bearing strength for the bushing must be calculated. The bushing ultimate load is given by:
where Dp is the pin diameter, t is the bushing thickness (assumed to be equal to the lug thickness), and Scy.B is the compressive yield strength of the bushing material. The Air Force manual assumes the compressive ultimate strength of the bushing material, Scu.B, to be equal to 1.304·Scy.B.
If there is no bushing in the lug, then the calculation should still be performed assuming that the lug material is the bushing material.
Net Section Strength Under Axial Load
The net-section ultimate load accounts for tension failure across the net section and is calculated by:
where w is the width and D is the hole diameter. Fnu.L and Fny.L are the ultimate and yield net-section stresses, respectively, and are given by the following equations:
| Ultimate Net-Section Stress: | Fnu.L = Kn Stu |
| Yield Net-Section Stress: | Fny.L = Kn Sty |
The factor Kn in the equations above is the net tension stress coefficient which is a knock-down on the allowable stresses. The value of Kn is determined by interpolating between the following plots:
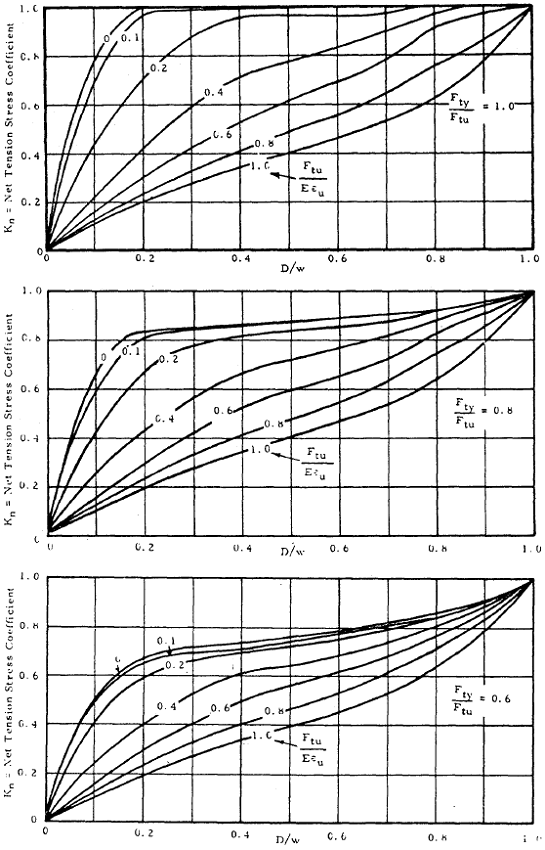
In the curves above, Fty and Ftu are the material's yield and ultimate strengths, respectively, E is the elastic modulus, and εu is the ultimate strain (i.e. the total strain at failure).
Design Strength Under Axial Load
The design ultimate load for an axially loaded lug is the minimum of the ultimate bearing load, the ultimate bushing load, and the ultimate net-section load:
Transverse Loading
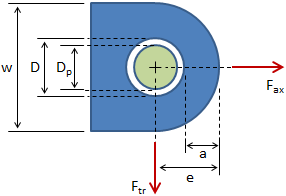
The analysis for a transversely loaded lug is similar to that for an axially loaded lug. However, the failure mode for transverse loading is more complicated than for axial loading, and different dimensions are critical for determining lug strength. The dimensions of interest for a transversely loaded lug are shown in the figure below:
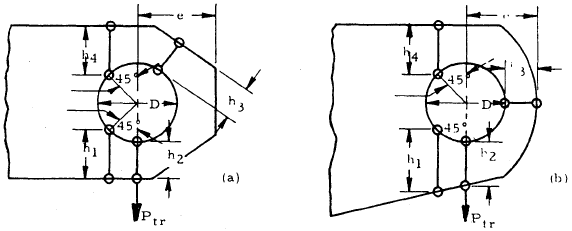
where h1, h2, h3, and h4 are failure planes of interest. If the lug is symmetric, then the values for these dimensions can be easily obtained from the dimensions for an axially loaded lug:
| h2 = 0.5 (w − D) |
| h1 = h4 = h2 + 0.5 D (1 − cos 45°) |
| h3 = a |
It should be noted that h3 is defined as the smallest dimension on any radial section around the hole, but it will typically be equal to a. From the above dimensions, the effective edge distance is calculated:
The equation above is simply a "reciprocal average" that gives more weighting to dimension h1 since that section takes most of the load. (Note 3)
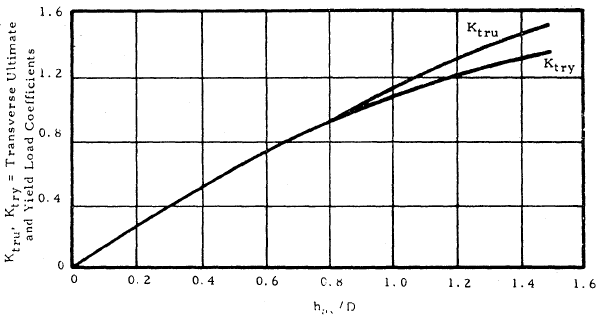
Lug Strength Under Transverse Load
The ultimate transverse load is given by:
where D is the hole diameter and t is the lug thickness. Fbru.L and Fbry.L are the lug ultimate and yield bearing stresses, respectively, and are given by the following equations:
| Ultimate Bearing Stress: | Fbru.L = Ktru Stu |
| Yield Bearing Stress: | Fbry.L = Ktry Sty |
where Ktru and Ktry are the transverse ultimate and yield load coefficients and are determined from the following plot:
Bushing Bearing Strength Under Transverse Load
The bearing strength for the bushing in a transversely loaded lug is the same as for an axially loaded lug:
where Pu.B is the bushing bearing strength for an axially loaded lug.
Design Strength Under Transverse Load
The design ultimate load for a transversely loaded lug is the minimum of the ultimate lug load and the ultimate bushing load:
Need a Lug Calculator?
Try our lug calculator based on the methodology described here.
- Allows for axial, transverse, or oblique loading
- Performs calculations for lug strength, pin strength, and double shear joint strength
Oblique Loading
In an obliquely loaded lug, the applied load has both axial and transverse components, as shown in the figure below:
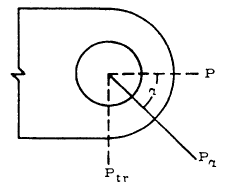
For an obliquely loaded lug, the applied load should be broken out into the axial and transverse components, Pax and Ptr, and the strengths in the axial and transverse directions should be calculated as discussed in the previous sections. An allowable load curve can then be defined which takes the form of an interaction equation, and is given below:
The allowable load curve defines the limits at which the lug is expected to fail -- it defines the ultimate load for a given combination of applied axial and transverse load. In the equation above, Pax.ult is the axial component of the ultimate load, Ptr.ult is the transverse component of the ultimate load, Pu.L.B is the design strength under axial load, and Ptru.L.B is the design strength under transverse load. The allowable load curve is shown below:
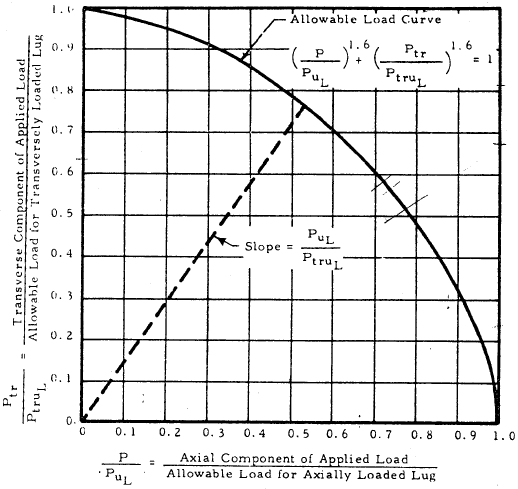
In the figure above, the values along the y-axis are the ratios of the transverse applied load to the transverse strength, and the values along the x-axis are the ratios of the axial applied load to the axial strength.
| Axial Load Ratio | Transverse Load Ratio |
|---|---|
|
|
|
The point for the applied load with coordinates of (Rax , Rtr) should be plotted. Any point that falls within the allowable load curve has a factor of safety ≥ 1 with respect to the ultimate load. Note that if the applied load is completely axial, then the value for Rtr is 0 and the point (Rax , Rtr) lies along the x-axis, and so the ultimate load is simply the axial design strength. Likewise for a completely transverse applied load; in this case, the point lies along the y-axis and so the ultimate load is the transverse design strength.
For an applied load with both axial and transverse components, the ultimate load is calculated by drawing a line from the origin, through the point (Rax , Rtr), and then through the allowable load curve. This is the load line, and it has a slope of:
The ultimate load ratios are given by the intersection of the load line with the allowable load curve. These ultimate ratios can then be used to calculate the ultimate load values in the axial and transverse directions.
| Ultimate Axial Load Ratio | Ultimate Transverse Load Ratio |
|---|---|
|
|
|
It should be noted that the equation for the slope given above disagrees with the slope specified in the Air Force Manual. A discussion is given in the Appendix.
Instead of determining the ultimate values by plotting, they can be calculated directly by noting that the ultimate load components, Pax.ult and Ptr.ult are related by:
where α is the angle of the applied load with respect to the axial direction. (Note 4) The equation defining the allowable load curve can then be solved for the ultimate axial load, with the relationship above substituted for the ultimate transverse load:
|
|
⟹ |
|
The ultimate applied load can then be determined by:
The factor of safety is calculated by: (Note 5)
Double Shear Joint Strength
It is important for the pin in the joint to be strong enough that it will distribute the load evenly over the lugs. Even though a weak pin will not commonly break in practice, excessive flexure of the pin will cause the load to "peak up" near the shear planes such that the outer edges of the lugs see high loads and the inner portions of the lugs are relatively unloaded. This can cause the material around the holes on the outer surfaces of the lugs to deform far enough to initiate a fracture, and the lug will fail at a lower load than predicted.
One effect that helps the situation is that as the load concentrates near the shear planes, the bending arm is reduced, and therefore the bending moment in the pin is reduced. However, a study cited by Molcon and Hoblit found that this decrease in bending moment is "seldom more than 25 percent and usually much less."
Since bending in the pin affects the strength of the lug, it is critical to account for the pin strength when analyzing the joint. In this section, a method for calculating the allowable load for a double shear joint is presented. An example of a double shear joint is shown below:
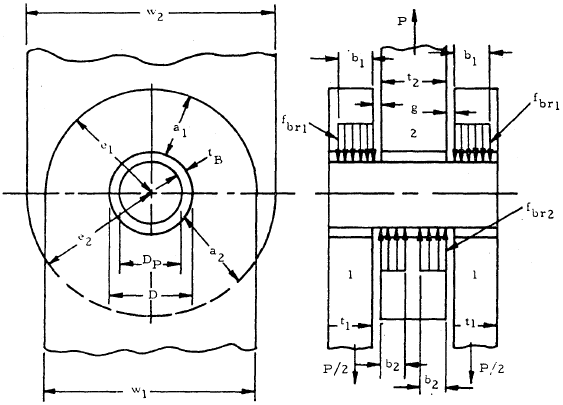
In a double shear joint, there are two outer (female) lugs, a single inner (male) lug, and a pin.
The overall process of determining the allowable load is illustrated in the diagram below:
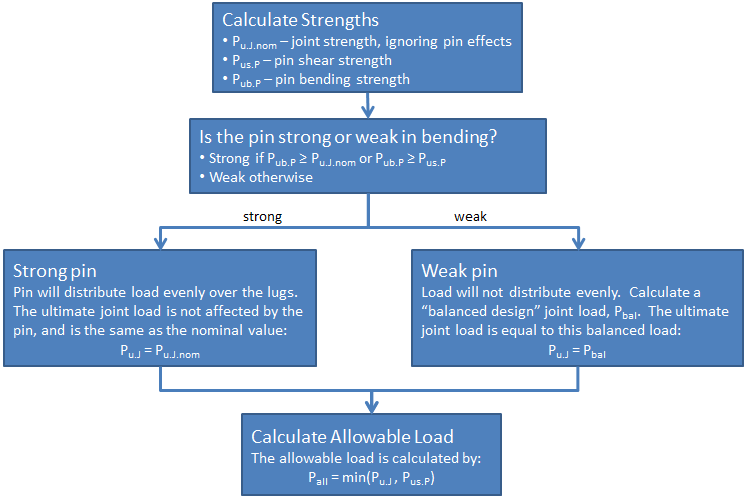
Calculate Joint Strength Ignoring Pin Effects
Initially ignoring the effects of pin bending, calculate the ultimate load of each lug in the joint using the methods described in the previous sections. Then calculate the nominal ultimate joint load (which does not account for the pin strength):
where Pult.M is the ultimate load for the male lug and Pult.F is the ultimate load for a single female lug. Since there are 2 female lugs supporting the load, then the ultimate load with respect to the female lugs is 2·Pult.F.
Calculate Pin Shear and Bending Strengths
The shear strength and the bending strength of the pin should both be calculated.
Pin Shear Strength
The ultimate shear load is calculated by:
where Dp is the pin diameter and Ssu.P is the ultimate shear strength of the pin material. Note that twice the area is used in calculating pin shear strength since there are two shear planes.
Pin Bending Strength
The ultimate bending load is the applied load that would result in bending failure of the pin, and is calculated by:
where Larm is the moment arm and Mu.P is the ultimate failing moment for the pin. If the load is distributed evenly across the entire width of the lugs, then the moment arm is calculated by:
where t1 is the thickness of a single female lug, t2 is the thickness of the male lug, and g is the gap between the male and female lugs when the male lug is centered between the female lugs.
The ultimate failing moment for the pin is calculated by:
where Stu.P is the ultimate tensile strength of the pin material and kb.P is the plastic bending coefficient. According to the Air Force Manual, "the value of kb.P varies from 1.0 for a perfectly elastic pin to 1.7 for a perfectly plastic pin, with a value of 1.56 for pins made from reasonably ductile materials (more than 5% elongation)."
Pin Strong or Weak in Bending?
Once the pin strengths are calculated, determine whether the pin is strong or weak in bending. If the pin ultimate bending load (Pub.P) is greater than either the pin ultimate shear load (Pus.P) or the nominal ultimate joint load (Pu.J.nom), then the pin is relatively strong and is not critical in bending. Otherwise, the pin is weak and is critical in bending.
| Pub.P ≥ Pu.J.nom or Pub.P ≥ Pus.P ? | Yes → Strong Pin |
| No → Weak Pin |
Strong Pin
If the pin is strong, the joint strength will be limited by either the pin shear strength or by the nominal joint strength. In the case of a strong pin, the pin ultimate bending load is calculated assuming that the load distributes evenly over the full width of the lugs:
The equation above is the same as the equation presented earlier for the ultimate pin bending load, but with the terms combined into a single equation.
For a strong pin, the pin bending does not affect the joint strength and the ultimate joint load is equal to the nominal ultimate joint load:
Weak Pin
If the pin is weak in bending, then the load will not be distributed evenly over the lug widths. Instead, the load will concentrate toward the shear planes, and the inner portions of the lugs will be relatively unloaded. Because of this, the lugs will fail at a lower load than predicted.
To account for the low pin bending strength, a "balanced design" ultimate load is calculated. The goal is to determine the actual bearing widths over which the lugs support the load. Instead of the load being supported over the full lug thicknesses, t1 and t2, the load will instead be distributed over some smaller widths, b1 and b2, as shown in the figure below. It is assumed that the load is uniformly distributed over these widths.

Reducing the bearing width has two effects:
- The ultimate load is reduced for the lugs (the lugs fail at a lower load).
- The moment arm for the pin is reduced, which increases the pin's ultimate bending load (the pin fails at a higher load).
The new, increased value of the pin ultimate bending load is calculated by:
where, in the equation above, b1 and 2·b2 were substituted for t1 and t2 from the previous pin bending equation.
The trick is to find the values of b1 and b2 that result in the "balanced design" ultimate load. To determine the balanced design ultimate load, reduce the bearing widths of each of the lugs until the ultimate load for the lugs are equal to one other as well as equal to the ultimate bending load of the pin. This requires an iterative process.
Once the balanced design ultimate load is found, the ultimate joint load and the pin ultimate bending load are each equal to the balanced load:
Calculate Allowable Load for Joint
The ultimate joint load (Pu.J) should have been calculated in one of the two previous sections, depending on whether the pin was strong or weak in bending:
| Strong pin: | Pu.J = Pu.J.nom |
| Weak pin: | Pu.J = Pbalanced |
The overall ultimate load accounting for both the ultimate joint load and the ultimate pin shear load is calculated by:
The factor of safety is calculated by:
Need a Lug Calculator?
Try our lug calculator based on the methodology described here.
- Allows for axial, transverse, or oblique loading
- Performs calculations for lug strength, pin strength, and double shear joint strength
ASME BTH Method
The ASME method of lug analysis is described in ASME BTH-1, "Design of Below-the-Hook Lifting Devices." This method considers the following failure modes, where the numbers correspond to the figure:
- Tension failure across the net section
- Shear failure along two planes
- Bearing failure
- Fracture on single plane

While the factor of safety on dishing (out-of-plane buckling) is not explicitly calculated, the effective width calculation accounts for the lug thickness in an attempt to protect against dishing failure.
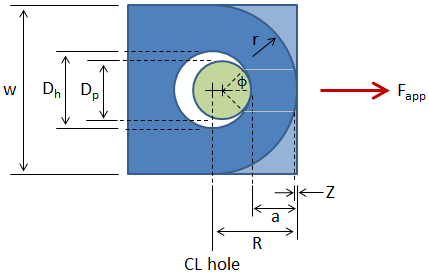
The dimensions of interest for the lug analysis are shown in the figure below:
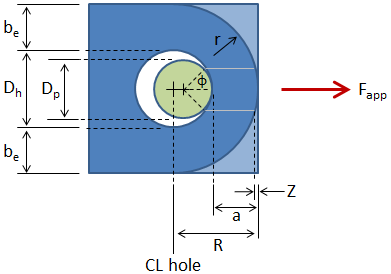
The dimensions from the figure include:
- Dh = hole diameter
- Dp = pin diameter
- be = net width (distance between the edge of the hole and the edge of the lug in the transverse direction)
- R = edge distance (distance from the center of the hole to the edge of the lug in the direction of applied load)
- r = radius of curvature of edge of lug (greater than or equal to R)
- a = distance from the edge of the hole to the edge of the lug = R − 0.5 Dh
- t = thickness (not shown in figure -- thickness is into the page)
- Z = loss in shear plane length due to curvature at the end of the lug
- ϕ = shear plane locating angle
Correction Factors
The analysis in ASME BTH is very similar to the simplified analysis, with the exception of several correction factors that are calculated based on test results. These correction factors are discussed below.
Strength Reduction Factor
The lug strength is reduced as the fit between the pin and the hole is loosened. The lug strength is not much affected as long as the pin and hole are a relatively tight fit. ASME defines a strength reduction factor that can be used to account for the pin-to-hole clearance as:
where Dp is the pin diameter and Dh is the hole diameter.
Shear Plane Locating Angle
A shear plane locating angle, ϕ, is used to locate the two planes along which shear tear out occurs, as shown in the figure:
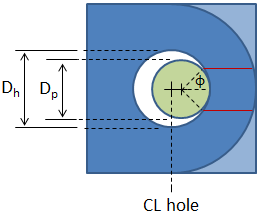
A larger value of ϕ results in a larger shear plane area. Other methodologies commonly take ϕ as a constant value (typically 40°), but ASME relates it to the ratio of the pin diameter to the hole diameter such that a loose-fitting pin has a smaller shear plane area than a tight-fitting pin:
Effective Width
The term be is referred to as the net width and is the distance between the edge of the hole and the edge of the lug in the transverse direction, as shown in the figure:
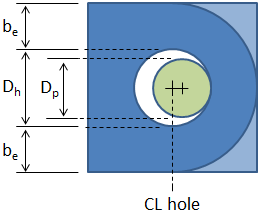
In the tension calculations, an effective width is calculated and is the smallest of the following:
| • | beff.1 = be | The effective width should not be larger than the actual net width. |
| • | beff.2 = 4 t | This limit is intended to protect against dishing failure (once the lug thickness drops below 1/4 of the net width be, the effective width is driven down). This limit can be ignored if the lug is stiffened or constrained against buckling. |
| • |
|
This equation is empirical, fitted to test results. |
The effective width is calculated as:
Design Factor & Service Class
A design factor (i.e. required factor of safety), Nd, is used in the strength calculations. The value for Nd can be found from the table below:
| Design Factor | Condition |
|---|---|
| Nd = 2.00 | Design Category A lifters (predictable loads, accurately defined or non-severe environmental conditions, no more than 20,000 load cycles) |
| Nd = 3.00 | Design Category B lifters (unpredictable loads, uncertain or severe environmental conditions) |
A service class is used to account for fatigue life and is defined based on the table below:
| Service Class | Load Cycles |
|---|---|
| 0 | 0 - 20,000 |
| 1 | 20,001 - 100,000 |
| 2 | 100,001 - 500,000 |
| 3 | 500,001 - 2,000,000 |
| 4 | Over 2,000,000 |
Lug Strength Calculations
These strength calculations are only applicable for axially applied loads, as indicated by the applied force arrow in the figure below:

To determine whether the lug has sufficient strength, calculate a factor of safety for each of the failure modes described below. As long as the applied force is within the allowable load, and as long as each factor of safety is acceptable, then the lug can be considered to pass.
Tensile Strength
The ultimate tensile load is the load that would result in tensile failure across the net section, and is given by:
where Cr is the strength reduction factor and Stu is the ultimate tensile strength of the lug. At is the area of the net section and is calculated by:
where beff is the effective width and t is the lug thickness.
The allowable tensile load is based on the design factor, Nd, and is given by:
Note that the allowable tensile load is based on the design factor multiplied by 1.20. ASME requires the design factor for some of the strength calculations to be higher than the nominal value. The factor of safety is given by:
To meet ASME BTH, the factor of safety must be at least 1.20·Nd, but the required factor of safety may be larger depending on customer requirements or engineering judgement.
Single Plane Fracture Strength
The ultimate single plane fracture load is the load that would result in failure along the plane collinear with the applied load, and is given by:
where Cr is the strength reduction factor and Stu is the ultimate tensile strength of the lug. Ab is an effective area that is calculated as:
where R is the edge distance, Dh is the hole diameter, be is the net width, and t is the lug thickness.
The allowable single plane fracture load is based on the design factor, Nd, and is given by:
The factor of safety is given by:
Double Plane Fracture Strength
The ultimate double plane shear load is the load that would result in shear tear out along the two planes, and is given by:
where Stu is the ultimate tensile strength of the lug. Av is the total area of the two shear planes and is given by:
where ϕ is the shear plane locating angle and Z is the loss in shear plane length due to the curvature at the end of the lug. This loss is calculated as:
Note that if the lug end is flat then r is infinity and Z is zero.
The allowable double plane shear load is based on the design factor, Nd, and is given by:
The factor of safety is given by:
Bearing Strength
The ultimate bearing load is the load that would result in bearing failure on either the lug or the pin. This ultimate load is dependent on the number of load cycles that the connection will be subjected to, and is given by:
where Sty.min is the minimum yield strength between the lug and the pin (i.e. Sty.min = min(Sty.lug , Sty.pin)). The value Ap is the pin bearing area and is calculated by:
The allowable bearing load is based on the design factor, Nd, and is given by:
The factor of safety is given by:
PDH Classroom offers a continuing education course based on this lug analysis reference page. This course can be used to fulfill PDH credit requirements for maintaining your PE license.
Now that you've read this reference page, earn credit for it!
Appendix
Discrepancy With Air Force Manual - Oblique Loading
The Air Force Manual specifies to calculate the factor of safety for an obliquely loaded lug by drawing a line from the origin that intersects with the allowable load curve, where the slope of the line is given by:
where Pu.L is the ultimate load for an axially loaded lug and Ptru.L is the ultimate load for a transversely loaded lug.
The problem with using the above equation for the slope is that the intersection line is the same regardless of the angle of the applied force. This problem is illustrated in the figure below:
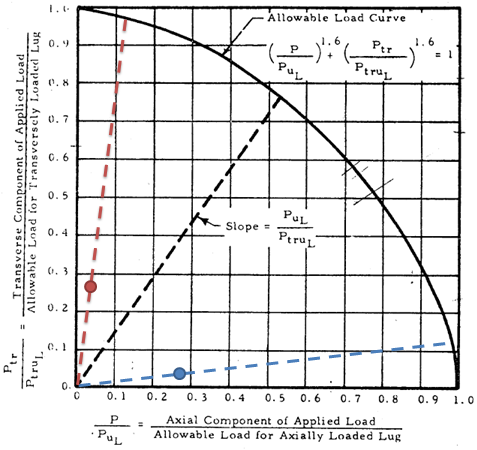
If the applied force is at an angle of 5° such that it is almost entirely axial, then the point for the applied load would lie along the blue line as shown in the figure, and the intersection point should reflect a factor of safety that is very close to that of a pure axially loaded lug. Likewise, if the applied force is at an angle of 85° such that it is almost entirely transverse, then the point for the applied load would lie along the red line as shown in the figure, and the intersection point should reflect a factor of safety that is very close to that of a pure transversely loaded lug. Based on this reasoning, the slope of the line should reflect the applied loading condition:
Notes
Note 1: Lug & Clevis Relative Sizing
It should be noted that the figure showing the lug with the clevis pin does not accurately depict the relative sizing. The clevis pin should be a relatively tight fit in the lug. Per ASME, the pin diameter should be at least 90% of the lug hole diameter to avoid a reduction in the joint strength.
Note 2: Axial Load Coefficient Plot
The variable names used in the Axial Load Coefficient plot from the Air Force Manual are inconsistent with the rest of the variable names throughout the manual. This plot originated in Melcon & Hoblit, and the variable names from the plot were not updated to match. The Air Force Manual uses the variable e for edge distance (center of hole to edge of lug) and a for the distance between the edge of the hole to the edge of the lug. However, the plot uses a for the edge distance (center of hole to edge of lug).
Note 3: Reciprocal Average for Transverse Lug Dimensions
The effective edge distance for a transversely loaded lug is calculated using a reciprocal average. The effect of the reciprocal average is that the result is dominated by the smaller terms such that a disproportionately large value will not drive up the average much, but a disproportionately small value will drop the average significantly (i.e. a weak link -- this is the same effect seen by placing springs in series). The use of this equation for calculating the effective edge distance for a transversely loaded lug originated with Melcon and Hoblit. They stated that the reason for the coefficient 3 on the h1 term was to reduce scatter on their test data, but that it made sense because in a transversely loaded lug the h1 section will be taking most of the load.
Note 4: Relationship Between Ultimate Load Components for Oblique Loading
To calculate the ultimate load components for an obliquely loaded lug, it is necessary to determine a relationship between the ultimate components. It is known that the actual load ratios are proportional to the ultimate load ratios since these ratios lie along the same load line:
Express the ratios in terms of the load components and simplify:
The load components are related by the angle of the applied load:
Note 5: Factor of Safety for Oblique Loading
It should be noted that the factor of safety for an obliquely loaded lug can be incorporated into the allowable load curve itself by:
The factor of safety can then be calculated directly by:
References
- ASME BTH-1, "Design of Below-the-Hook Lifting Devices," The American Society of Mechanical Engineers, 2014.
- Bruhn, E.F., "Analysis and Design of Flight Vehicle Structures," June 1973.
- Melcon, M.A and F.M. Hoblit, "Development in the Analysis of Lugs and Shear Pins," Product Engineering, June 1953.
- Niu, Michael C., "Airframe Stress Analysis and Sizing," October 2011.
- "Stress Analysis Manual," Air Force Flight Dynamics Laboratory, October 1986.