Mechanical Properties of Materials
The mechanical properties of a material affect how it behaves as it is loaded. The elastic modulus of the material affects how much it deflects under a load, and the strength of the material determines the stresses that it can withstand before it fails. The ductility of a material also plays a significant role in determining when a material will break as it is loaded beyond its elastic limit. Because every mechanical system is subjected to loads during operation, it is important to understand how the materials that make up those mechanical systems behave.
This page describes the mechanical properties of materials that are relevant to the design and analysis of mechanical systems.
Contents
Stress and Strain
The relationship between stress and strain in a material is determined by subjecting a material specimen to a tension or compression test. In this test, a steadily increasing axial force is applied to a test specimen, and the deflection is measured as the load is increased. These values can be plotted as a load-deflection curve. The deflection in the test specimen is dependent on both the material's elastic modulus as well as the geometry of the specimen (area and length). Since we are interested material behavior without regard to geometry, it is useful to generalize the data to remove the effect of geometry. This is done by converting the load values to stress values and converting the deflection values to strain values:
| Stress: |
|
| Strain: |
|
In the equation for stress, P is the load and A0 is the original cross-sectional area of the test specimen. In the equation for strain, L is the current length of the specimen and L0 is the original length.
Stress-Strain Curve
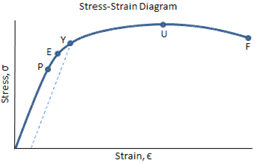
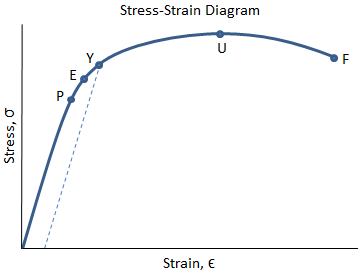
The values of stress and strain determined from the tensile test can be plotted as a stress-strain curve, as shown below:
Check out our Stress-Strain Curve calculator based on the methodology described here.
There are several points of interest in the diagram above:
- P: This is the proportionality limit, which represents the maximum value of stress at which the stress-strain curve is linear.
- E: This is the elastic limit, which represents the maximum value of stress at which there is no permanent set. Even though the curve is not linear between the proportionality limit and the elastic limit, the material is still elastic in this region and if the load is removed at or below this point the specimen will return to its original length.
- Y: This is the yield point, which represents the value of stress above which the strain will begin to increase rapidly. The stress at the yield point is called the yield strength, Sty. For materials without a well-defined yield point, it is typically defined using the 0.2% offset method in which a line parallel to the linear portion of the curve is drawn that intersects the x-axis at a strain value of 0.002. The point at which the line intersects the stress-strain curve is designated as the yield point.
- U: This point corresponds to the ultimate strength, Stu, which is the maximum value of stress on the stress-strain diagram. The ultimate strength is also referred to as the tensile strength. After reaching the ultimate stress, specimens of ductile materials will exhibit necking, in which the cross-sectional area in a localized region of the specimen reduces significantly.
- F: This is the fracture point or the break point, which is the point at which the material fails and separates into two pieces.
Stress-strain curves are commonly needed when analyzing an engineered component. However, stress-strain data may not always be readily available. In this case, it is fairly straightforward to approximate a material's stress-strain curve using the Ramberg-Osgood equation.
True Stress and Strain
Engineers typically work with engineering stress, which is the force divided by the original area of the specimen before loading: σ = P/A0. However, as a material is loaded, the area decreases. The true stress, , is the value of stress in the material considering the actual area of the specimen. Because the area decreases as a material is loaded, true stress is higher than engineering stress.
The figure below shows an engineering stress-strain curve as compared to a true stress-strain curve. Because the engineering stress is calculated as force divided by original area (which is a constant), the engineering stress-strain curve has the same shape as the load-deflection curve. The engineering stress-strain curve drops after the ultimate strength is reached because the force that can be supported by the material drops as it begins to neck down. However, the stress value in the true stress-strain curve always increases as the strain increases. This is because the instantaneous value of area is used when calculating true stress. Even when the force supported by the material drops, the reduction in the specimen area outweighs the reduction in force, and the stress continues to increase.
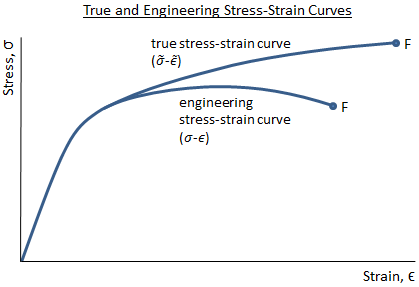
It should be noted that the engineering stress and the true stress are essentially the same in the linear-elastic region of the stress-strain curve. Because engineers typically operate within this linear-elastic region (it is uncommon to design a structure that is intended to operate beyond the elastic limit), it is valid to work with engineering stress as opposed to true stress.
Engineering strain is the change in length divided by the original length: ε = ΔL/L0. Instead of just calculating a single value of ΔL, consider that the change in length is divided among many small increments, ΔLj. The strain is also calculated in small increments: εj = ΔLj/Lj, where ΔLj is the change in length for an increment, and Lj is the length at the start of the increment. As these increments become infinitesimally small, the summation of the strains approaches the true strain, :
If it is assumed that the volume is constant throughout the deflection, then true stress and strain can be calculated as:
| True Stress: |
|
| True Strain: |
|
where and are the true stress and strain, and σ and ε are the engineering stress and strain.
Hooke's Law
Below the proportionality limit of the stress-strain curve, the relationship between stress and strain is linear. The slope of this linear portion of the stress-strain curve is the elastic modulus, E, also referred to as the Young's modulus and the modulus of elasticity. Hooke's law expresses the relationship between the elastic modulus, the stress, and the strain in a material within the linear region:
where σ is the value of stress and ε is the value of strain.
Hooke's Law in Shear
Hooke's law also has a form relating shear stresses and strains:
where τ is the value of shear stress, γ is the value of shear strain, and G is the shear modulus of elasticity. The elastic modulus and the shear modulus are related by:
where ν is Poisson's ratio.
More information on Hooke's law can be found here.
Poisson's Ratio
As load is applied to a material, the material elongates and the cross-sectional area is reduced. This reduction in cross-sectional area is called lateral strain, and it is related to the axial strain by Poisson's ratio, ν. For a circular specimen this reduction in area is realized as a reduction in diameter, and the Poisson's ratio is calculated as:
Poisson's ratio only applies within the elastic region of the stress-strain curve, and it is typically about 0.3 for most metals. The theoretical maximum limit of Poisson's ratio is 0.5.
We have a number of structural calculators to choose from. Here are just a few:
Strain Hardening
After a material yields, it begins to experience a high rate of plastic deformation. Once the material yields, it begins to strain harden which increases the strength of the material. In the stress-strain curves below, the strength of the material can be seen to increase between the yield point Y and the ultimate strength at point U. This increase in strength is the result of strain hardening.
The ductile material in the figure below is still able to support load even after the ultimate strength is reached. However, after the ultimate strength at point U, the increase in strength due to strain hardening is outpaced by the reduction in load-carrying ability due to the decrease in cross sectional area. Between the ultimate strength at point U and the fracture point F, the engineering strength of the material decreases and necking occurs.
In the stress-strain curve for the brittle material below, a very small region of strain hardening is shown between the yield point Y and the ultimate strength U. Note however that a brittle material may not actually exhibit any yielding behavior or strain hardening at all -- in this case, the material would fail on the linear portion of the curve. This is more common in materials such as ceramics or concrete.
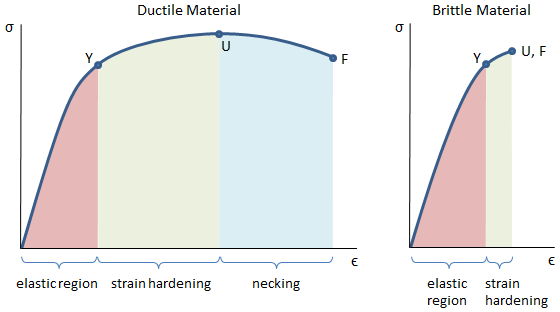
Because the strain hardening region occurs between the yield point and the ultimate point, the ratio of the ultimate strength to the yield strength is sometimes used as a measure of the degree of strain hardening in a material. This ratio is the strain hardening ratio:
According to Dowling, typical values of strain hardening ratio in metals range from approximately 1.2 to 1.4.
If a material is loaded beyond the elastic limit, it will undergo permanent deformation. After unloading the material, the elastic strain will be recovered (return to zero) but the plastic strain will remain.
The figure below shows the stress-strain curve of a material that was loaded beyond the yield point, Y. The first time the material was loaded, the stress and strain followed the curve O-Y-Y', and then the load was removed once the stress reached the point Y'. Since the material was loaded beyond the elastic limit, only the elastic portion of the strain is recovered -- there is some permanent strain now in the material. If the material were to be loaded again, it would follow line O'-Y'-F, where O'-Y' is the previous unloading line. The point Y' is the new yield point. Note that the line O'-Y' is linear with a slope equal to the elastic modulus, and the point Y' has a higher stress value than point Y. Therefore, the material now has a higher yield point than it had previously, which is a result of strain hardening that occurred by loading the material beyond the elastic limit.
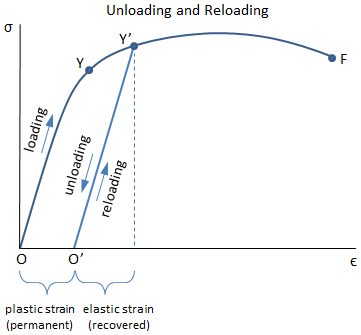
By strain hardening the material, it now has a larger elastic region and a higher yield stress, but its ductility has been reduced (the strain between points Y'-F is less than the strain between points Y-F).
Elastic and Plastic Strain
Up to the elastic limit, the strain in the material is also elastic and will be recovered when the load is removed so that the material returns to its original length. However, if the material is loaded beyond the elastic limit, then there will be permanent deformation in the material, which is also referred to as plastic strain.
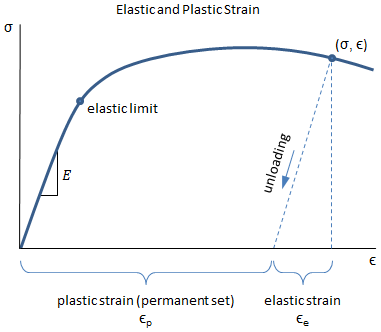
In the figure above, both elastic and plastic strains exist in the material. If the load is removed at the indicated point (σ, ε), the stress and strain in the material will follow the unloading line as shown. The elastic strain and plastic strain are indicated in the figure, and are calculated as:
| Elastic Strain: | εe = σ/E |
| Plastic Strain: | εp = ε − εe |
where σ is the stress at the indicated point, ε is the strain at the indicated point, and E is the elastic modulus.
Ductility
Ductility is an indication of how much plastic strain a material can withstand before it breaks. A ductile material can withstand large strains even after it has begun to yield. Common measures of ductility include percent elongation and reduction in area, as discussed in this section.
After a specimen breaks during a tensile test, the final length of the specimen is measured and the plastic strain at failure, also known as the strain at break, is calculated:
where Lf is the final length of the specimen after break and Lo is the initial length of the specimen. It is important to note that after the specimen breaks, the elastic strain that existed while the specimen was under load is recovered, so the measured difference between the final and initial lengths gives the plastic strain at failure. This is illustrated in the figure below:
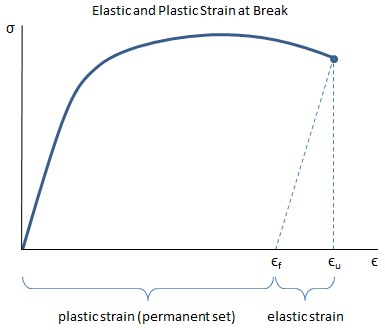
In the figure, it can be seen that the plastic strain at failure, εf, is the strain remaining in the material after the elastic strain has been recovered. The ultimate strain, εu, is the total strain at failure (the plastic strain plus the elastic strain).
The percent elongation is calculated from the plastic strain at failure by:
The percent elongation is a commonly provided material property, so the plastic strain at failure is typically calculated from percent elongation:
The ultimate strain accounts for both plastic and elastic strain at failure:
Another important material property that can be measured during a tensile test is the reduction in area, which is calculated by:
Remember that percent elongation and reduction in area account for the plastic components of the axial strain and the lateral strain, respectively.
We have a number of structural calculators to choose from. Here are just a few:
Ductile and Brittle Materials
A ductile material can withstand large strains even after it has begun to yield, whereas a brittle material can withstand little or no plastic strain. The figure below shows representative stress-strain curves for a ductile material and a brittle material.
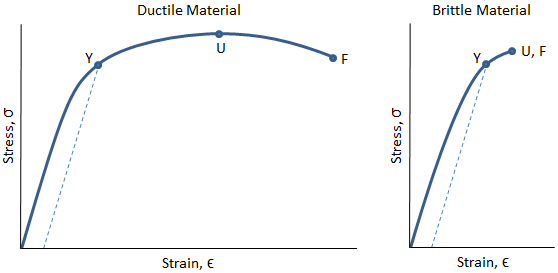
In the figure above, the ductile material can be seen to strain significantly before the fracture point, F. There is a long region between the yield at point Y and the ultimate strength at point U where the material is strain hardening. There is also a long region between the ultimate strength at point U and the fracture point F in which the cross sectional area of the material is decreasing rapidly and necking is occurring.
The brittle material in the figure above can be seen to break shortly after the yield point. Additionally, the ultimate strength is coincident with the fracture point. In this case, no necking occurs.
Because the area under the stress-strain curve for the ductile material above is larger than the area under the stress-strain curve for the brittle material, the ductile material has a higher modulus of toughness -- it can absorb much more strain energy before it breaks. Additionally, because the ductile material strains so significantly before it breaks, its deflections will be very high before failure. Therefore, it will be visually apparent that failure is imminent, and actions can be taken to resolve the situation before disaster occurs.
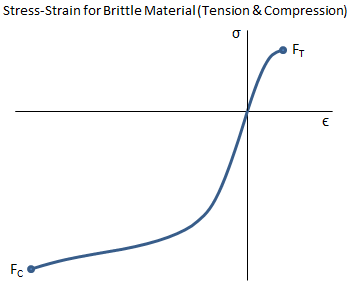
A representative stress-strain curve for a brittle material is shown below. This curve shows the stress and strain for both tensile and compressive loading. Note how the material is much more resistant to compression than to tension, both in terms of the stress that it can withstand as well as the strain before failure. This is typical for a brittle material.
Strain Energy
When force is applied to a material, the material deforms and stores potential energy, just like a spring. The strain energy (i.e. the amount of potential energy stored due to the deformation) is equal to the work expended in deforming the material. The total strain energy corresponds to the area under the load deflection curve, and has units of in-lbf in US Customary units and N-m in SI units. The elastic strain energy can be recovered, so if the deformation remains within the elastic limit, then all of the strain energy can be recovered.
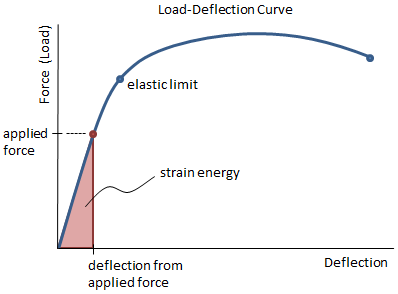
Strain energy is calculated as:
| General Form: | U = Work = ∫ F dL | (area under load-deflection curve) |
| Within Elastic Limit: |
|
(area under load-deflection curve) |
|
|
(spring potential energy) |
Note that there are two equations for strain energy within the elastic limit. The first equation is based on the area under the load deflection curve. The second equation is based on the equation for the potential energy stored in a spring. Both equations give the same result, they are just derived somewhat differently.
Strain Energy Density
It is sometimes more convenient to work with strain energy density, which is the strain energy per unit volume. This is equal to the area under the stress-strain diagram:
where the limits in the integral above are from a strain of 0 to εapp, which is the strain existing in the loaded material.
Note that the units of strain energy density are psi in US Customary units and Pa in SI units.
Modulus of Resilience
The modulus of resilience is the amount of strain energy per unit volume (i.e. strain energy density) that a material can absorb without permanent deformation resulting. The modulus of resilience is calculated as the area under the stress-strain curve up to the elastic limit. However, since the elastic limit and the yield point are typically very close, the resilience can be approximated as the area under the stress-strain curve up to the yield point. Since the stress-strain curve is very nearly linear up to the elastic limit, this area is triangular.
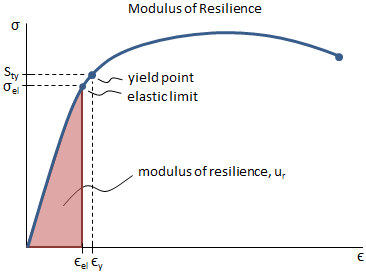
The modulus of resilience is calculated as:
|
|
general form |
|
|
triangular form |
where σel and εel are the stress and strain at the elastic limit, Sty is the tensile yield strength, and E is the elastic modulus.
Note that the units of the modulus of resilience are the same as the units of strain energy density, which are psi in US Customary units and Pa in SI units.
Modulus of Toughness
The modulus of toughness is the amount of strain energy per unit volume (i.e. strain energy density) that a material can absorb just before it fractures. The modulus of toughness is calculated as the area under the stress-strain curve up to the fracture point.
An accurate calculation of the total area under the stress-strain curve to determine the modulus of toughness is somewhat involved. However, a rough approximation can be made by dividing the stress-strain curve into a triangular section and a rectangular section, as seen in the figure below. The height of the sections is equal to the average of the yield strength and the ultimate strength.
The modulus of toughness can be approximated as:
where Sty is the tensile yield strength, Stu is the tensile ultimate strength, εy is the strain at yield, εu is the ultimate strain (total strain at failure), and E is the elastic modulus.
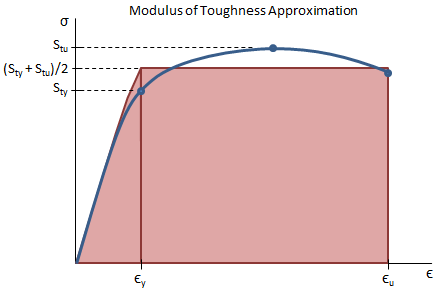
A better calculation of the modulus of toughness could be made by using the Ramberg-Osgood equation to approximate the stress-strain curve, and then integrating the area under the curve.
It should be noted how greatly the area under the plastic region of the stress-strain curve (i.e. the rectangular portion) contributes to the toughness of the material. Since a ductile material can withstand much more plastic strain than a brittle material, a ductile material will therefore have a higher modulus of toughness than a brittle material with the same yield strength. Even though structures are typically designed to keep stresses within the elastic region, a ductile material with a higher modulus of toughness is better suited to applications in which an accidental overload may occur.
Note that the units of the modulus of toughness are the same as the units of strain energy density, which are psi in US Customary units and Pa in SI units.
We have a number of structural calculators to choose from. Here are just a few:
Stress-Strain Curve Approximation
Stress-strain curves for materials are commonly needed; however, without representative test data it is necessary to come up with an approximation of the curve. The Ramberg-Osgood equation can be used to approximate the stress-strain curve for a material knowing only the yield strength, ultimate strength, elastic modulus, and percent elongation of the material (all of which are common and readily available properties).
Check out our Stress-Strain Curve calculator based on the methodology described here.
The Ramberg-Osgood equation for total strain (elastic and plastic) as a function of stress is:
where σ is the value of stress, E is the elastic modulus of the material, Sty is the tensile yield strength of the material, and n is the strain hardening exponent of the material, which can be calculated from known material properties as shown later in this section. (Note 1)
An explanation of the derivation of the Ramberg-Osgood equation is provided in the following sections.
Ramberg-Osgood Equation
A relationship was proposed by Ramberg and Osgood that is frequently used to approximate the stress-strain curve for a material. This relationship is exponential and is used to describe the plastic strain in a material. The stress-strain curve in the plastic region can be approximated by:
| σ = H εpn | ⟹ |
|
where, in the equation above, εp is the plastic strain, H is the strength coefficient with the same units as stress, and n is the strain hardening exponent and is unitless.
The elastic strain in a material is linearly proportional to stress:
| σ = E εe | ⟹ | εe = σ/E |
where, in the equation above, εe is the elastic strain and E is the elastic modulus.
The total strain in a material is the summation of the elastic strain and the plastic strain:
| ε = εe + εp | ⟹ |
|
Determining Constants for Ramberg-Osgood
For the Ramberg-Osgood equation to be useful, values for the constants n and H must be known. A discussion of how to determine the constants for an exponential equation is given here.
The constants are found by:
where, in the equations above, (σ1, ε1) and (σ2, ε2) correspond to two points within the plastic region of the stress-strain curve. The task at hand then is to find those two points so that the constants may be calculated.
If the yield strength (Sty), ultimate strength (Stu), elastic modulus (E), and plastic strain at failure (εf) for a material are known, then two points within the plastic region can be determined (the yield and ultimate points), and from those points the plastic region curve can be calculated. Remember that the plastic strain at failure can be calculated from the percent elongation, eL, by εf = eL/100%. Luckily all of these properties are commonly known for a material.
It is important to note that the equation for the plastic region curve, σ = H εpn, is dependent on plastic strain, and so we will need to determine the values of plastic strain for the two points of interest. Plastic strain can be calculated from total strain using:
where, in the equation above, ε is the total strain and εe is the elastic strain.
The table below is used to determine the yield point and the ultimate point:
| Stress, σ | Total Strain, ε | Elastic Strain, εe | Plastic Strain, εp | |
|---|---|---|---|---|
| Yield Point: | Sty | Sty/E + 0.002 | Sty/E | 0.002 |
| Ultimate Point: | Stu | Stu/E + εf | Stu/E | εf |
Note that when determining the strain at the yield point, a plastic strain of 0.002 was assumed. This is consistent with the 0.2% offset method, as described previously. This assumption is necessary in order to place the yield point within the plastic region of the curve. From the table above, it can be seen that the yield point and ultimate point within the plastic region are given by:
| • | Yield Point: | (Sty, 0.002) |
| • | Ultimate Point: | (Stu, εf) |
From the two points in the plastic region of the curve, the constants n and H for the Ramberg-Osgood equation can be calculated. The strain hardening exponent, n, is calculated as: (Note 1)
The value for H is calculated using the yield point, (Sty, 0.002), as the point of reference, although either point would do:
Now that the constants n and H have been determined, the equation for the total strain as a function of stress is known:
The equation above can be simplified by substituting the expression for H. The final equation for total strain as a function of stress is:
PDH Classroom offers a continuing education course based on this mechanical properties of materials reference page. This course can be used to fulfill PDH credit requirements for maintaining your PE license.
Now that you've read this reference page, earn credit for it!
Notes
Note 1: Strain Hardening Exponent in Ramberg-Osgood Equation
The strain hardening exponent, denoted by n, should not be confused with the Ramberg-Osgood parameter, which is also denoted by n. The two parameters are reciprocals of one another, which only adds to the confusion. We use the strain hardening exponent in the Ramberg-Osgood equation rather than the Ramberg-Osgood parameter. The reason that we use the strain hardening exponent is that it is a general material property that is useful outside the context of the Ramberg-Osgood equation.
References
General References:
- Budynas-Nisbett, "Shigley's Mechanical Engineering Design," 8th Ed.
- Dowling, Norman E., "Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue," 3rd Ed.
- Gere, James M., "Mechanics of Materials," 6th Ed.
- Hibbeler, Russell C., "Mechanics of Materials," 10th Ed.
- Lindeburg, Michael R., "Mechanical Engineering Reference Manual for the PE Exam," 13th Ed.
Specifications and Standards:
- ASTM E8, "Standard Test Methods for Tension Testing of Metallic Materials," American Society for Testing and Materials, 2011.