The tables below give equations for the deflection, slope, shear, and moment along straight beams for different end conditions and loadings. You can find comprehensive tables in references such as Gere, Lindeburg, and Shigley. However, the tables below cover most of the common cases.

For information on beam deflection, see our reference on stresses and deflections in beams.

Cantilever Beams

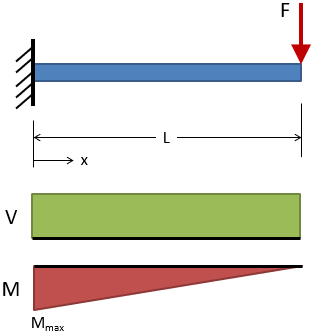
Cantilever, End Load		Deflection: @ x = L Slope: @ x = L Shear: V = +F Moment: M = −F (L − x) Mmax = −FL @ x = 0
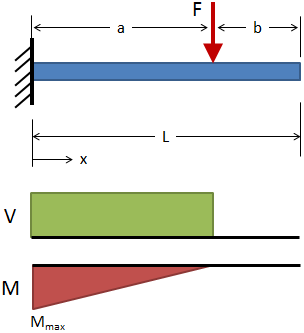
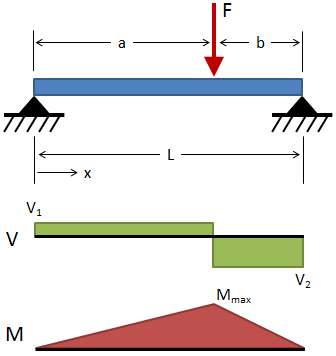
Cantilever, Intermediate Load		Deflection: ( 0 ≤ x ≤ a ) ( a ≤ x ≤ L ) @ x = L Slope: ( 0 ≤ x ≤ a ) ( a ≤ x ≤ L ) Shear: V = +F ( 0 ≤ x ≤ a ) V = 0 ( a ≤ x ≤ L ) Moment: M = −F (a − x) ( 0 ≤ x ≤ a ) M = 0 ( a ≤ x ≤ L )
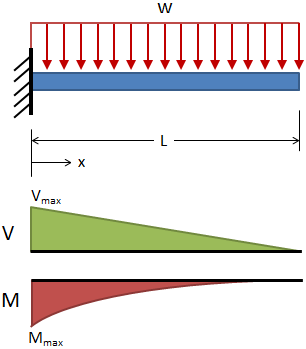
Cantilever, Uniform Distributed Load		Deflection: @ x = L Slope: @ x = L Shear: V = +w (L − x) Vmax = +wL @ x = 0 Moment: M = −w (L − x)2 / 2 Mmax = −wL2 / 2 @ x = 0
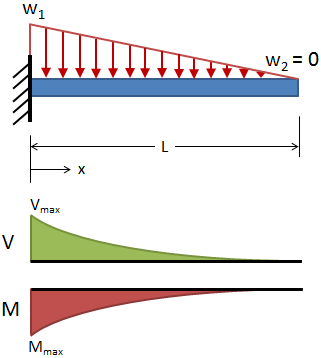
Cantilever, Triangular Distributed Load		Deflection: @ x = L Slope: @ x = L Shear: Vmax = +w1L / 2 @ x = 0 Moment: Mmax = −w1L2 / 6 @ x = 0
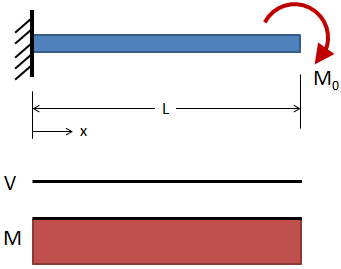
Cantilever, End Moment		Deflection: @ x = L Slope: @ x = L Shear: V = 0 Moment: M = −M0

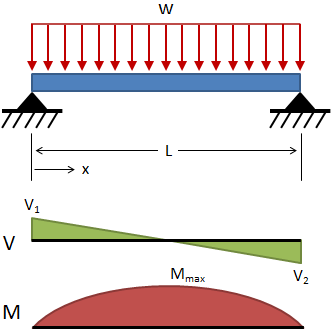
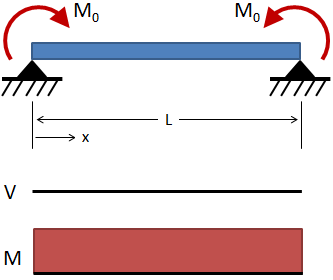
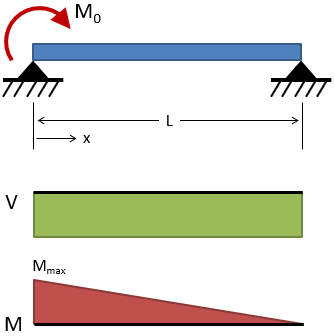
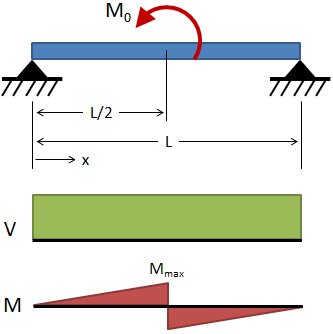
Simply Supported Beams

Simply Supported, Intermediate Load		Deflection: ( 0 ≤ x ≤ a ) For a ≥ b: @ Slope: ( 0 ≤ x ≤ a ) @ x = 0 @ x = L Shear: V1 = +Fb / L ( 0 ≤ x ≤ a ) V2 = −Fa / L ( a ≤ x ≤ L ) Moment: Mmax = +Fab / L @ x = a
Simply Supported, Center Load		Deflection: ( 0 ≤ x ≤ L/2 ) @ x = L/2 Slope: ( 0 ≤ x ≤ L/2 ) @ x = 0 @ x = L Shear: V1 = +F / 2 ( 0 ≤ x ≤ L/2 ) V2 = −F / 2 ( L/2 ≤ x ≤ L ) Moment: Mmax = FL / 4 @ x = L/2
Simply Supported, 2 Loads at Equal Distances from Supports		Deflection: ( 0 ≤ x ≤ a ) ( a ≤ x ≤ L − a ) @ x = L/2 Slope: ( 0 ≤ x ≤ a ) ( a ≤ x ≤ L − a ) @ x = 0 @ x = L Shear: V1 = +F ( 0 ≤ x ≤ a ) V2 = −F ( L − a ≤ x ≤ L ) Moment: Mmax = Fa ( a ≤ x ≤ L − a )
Simply Supported, Uniform Distributed Load		Deflection: @ x = L/2 Slope: @ x = 0 @ x = L Shear: V = w (L/2 − x) V1 = +wL / 2 @ x = 0 V2 = −wL / 2 @ x = L Moment: Mmax = wL2 / 8 @ x = L/2
Simply Supported, Moment at Each Support		Deflection: @ x = L/2 Slope: @ x = 0 @ x = L Shear: V = 0 Moment: M = M0
Simply Supported, Moment at One Support		Deflection: @ x = L (1 − √3/3) Slope: @ x = 0 @ x = L Shear: V = −M0 / L Moment: Mmax = M0 @ x = 0
Simply Supported, Center Moment		Deflection: ( 0 ≤ x ≤ L/2 ) Slope: ( 0 ≤ x ≤ L/2 ) @ x = 0 @ x = L Shear: V = +M0 / L Moment: M = M0x / L ( 0 ≤ x ≤ L/2 ) Mmax = M0 / 2 @ x = L/2

Fixed-Fixed Beams

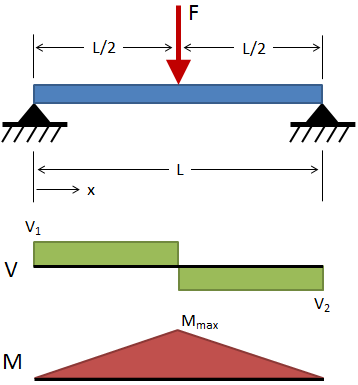
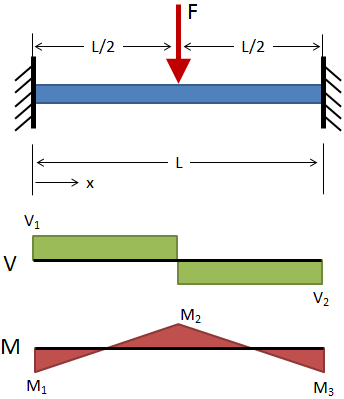
Fixed-Fixed, Center Load		Deflection: ( 0 ≤ x ≤ L/2 ) @ x = L/2 Shear: V1 = +F / 2 ( 0 ≤ x ≤ L/2 ) V2 = −F / 2 ( L/2 ≤ x ≤ L ) Moment: M = F (4x − L) / 8 ( 0 ≤ x ≤ L/2 ) M1 = M3 = −FL / 8 @ x = 0 & x = L M2 = +FL / 8 @ x = L/2
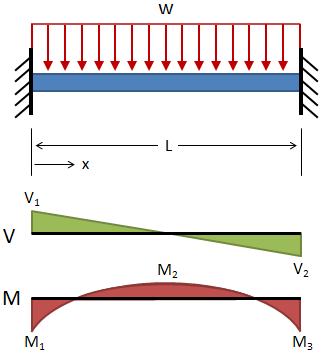
Fixed-Fixed, Uniform Distributed Load		Deflection: @ x = L/2 Shear: V = w (L/2 − x) V1 = +wL / 2 @ x = 0 V2 = −wL / 2 @ x = L Moment: M = w (6Lx − 6x2 − L2) / 12 M1 = M3 = −wL2 / 12 @ x = 0 & x = L M2 = wL2 / 24 @ x = L/2

---

---

References

1. Budynas-Nisbett, "Shigley's Mechanical Engineering Design," 8th Ed.
2. Gere, James M., "Mechanics of Materials," 6th Ed.
3. Lindeburg, Michael R., "Mechanical Engineering Reference Manual for the PE Exam," 13th Ed.

---