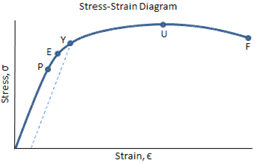
The Stress-Strain Curve calculator allows for the calculation of the engineering stress-strain curve of a material using the Ramberg-Osgood equation. See the reference section for details on the methodology and the equations used.

Material Property Inputs

Enter the material properties in either US or SI units:

Points for Stress-Strain Curve

The points for the engineering stress-strain curve are shown below:

Display Units:

Custom (Edit)

Yield Point			Ultimate Point
Yield Strength:			Ultimate Strength:
Yield Strain:			Ultimate Strain:

Ramberg-Osgood Equation

The stress-strain curve is approximated using the Ramberg-Osgood equation, which calculates the total strain (elastic and plastic) as a function of stress:

where σ is the value of stress, E is the elastic modulus of the material, S_ty is the tensile yield strength of the material, and n is the strain hardening exponent of the material which can be calculated based on the provided inputs.

Based on the specified material properties, the value of the strain hardening exponent, n, is:

n =

strain hardening exponent

Strain Values at Yield and Ultimate Strength Points

The strain value associated with the yield strength is:

Reference Values

S_ty	=
E	=

Note that a plastic strain of 0.002 is assumed. This is consistent with the 0.2% offset method, as described here.

The strain value associated with the ultimate strength is:

Reference Values

S_ty	=
E	=
ε_f	=

where ε_f is the plastic strain at failure and is simply the percent elongation expressed in decimal form:

ε_f = eL / 100% =

Reference Values

Need More Functionality?

Sign up for an account to receive full access to all calculators and other content. The subscription types are described below, along with the benefits of each.