This page provides a set of interactive plots for common stress concentration factors. See the reference section for more details.

Central Hole, Axial Central Hole, Bending U-Notches, Axial U-Notches, Bending Fillet, Axial Fillet, Bending

Rectangular Bar With Central Hole, Axial Force

This tab defines the stress concentration factor for a bar with a rectangular cross section and a central circular hole. The bar has an applied axial force (tensile or compressive).

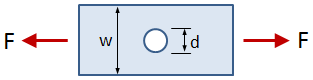
w = bar width
d = hole diameter
t = bar thickness
F = applied force (tensile or compressive)

The maximum stress is calculated as σ_max = K_t σ_nom, where K_t is the stress concentration factor as determined from the plot below, and σ_nom is calculated as:

Input Geometry:

Results:

d/w:

K_t:

The value of the stress concentration factor is calculated by:

Sources:

Rectangular Bar With Central Hole, Out-of-Plane Bending

This tab defines the stress concentration factor for a bar with a rectangular cross section and a central circular hole. The bar has an applied out-of-plane bending moment.

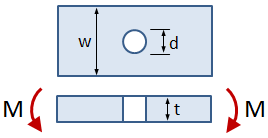
w = bar width
d = hole diameter
t = bar thickness
M = applied bending moment

The maximum stress is calculated as σ_max = K_t σ_nom, where K_t is the stress concentration factor as determined from the plot below, and σ_nom is calculated as:

Input Geometry:

Results:

d/t:

d/w:

K_t:

The value of the stress concentration factor is calculated by:

Sources:

Rectangular Bar With U-Notches, Axial Force

This tab defines the stress concentration factor for a bar with a rectangular cross section and two U-notches. The bar has an applied axial force (tensile or compressive).

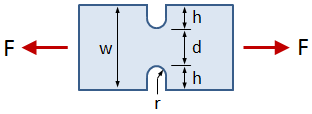
w = bar width
h = notch height
r = notch radius
t = bar thickness
F = applied force (tensile or compressive)

The maximum stress is calculated as σ_max = K_t σ_nom, where K_t is the stress concentration factor as determined from the plot below, and σ_nom is calculated as:

Input Geometry:

Results:

w/d:

r/d:

h/r:

K_t:

The value of the stress concentration factor is calculated by:

where the coefficients in the equation above are calculated from "Peterson's Stress Concentration Factors":

	0.1 ≤ h/r ≤ 2.0	2.0 ≤ h/r ≤ 50.0
C₁	0.955 + 2.169 √h/r − 0.081 (h/r)	1.037 + 1.991 √h/r + 0.002 (h/r)
C₂	−1.557 − 4.046 √h/r + 1.032 (h/r)	−1.886 − 2.181 √h/r − 0.048 (h/r)
C₃	4.013 + 0.424 √h/r − 0.748 (h/r)	0.649 + 1.086 √h/r + 0.142 (h/r)
C₄	−2.461 + 1.538 √h/r − 0.236 (h/r)	1.218 − 0.922 √h/r − 0.086 (h/r)

Sources:

Rectangular Bar With U-Notches, Bending

This tab defines the stress concentration factor for a bar with a rectangular cross section and two U-notches. The bar has an applied in-plane bending moment.

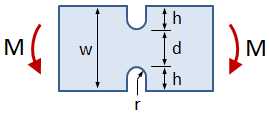
w = bar width
h = notch height
r = notch radius
t = bar thickness
M = applied bending moment

The maximum stress is calculated as σ_max = K_t σ_nom, where K_t is the stress concentration factor as determined from the plot below, and σ_nom is calculated as:

Input Geometry:

Results:

w/d:

r/d:

h/r:

K_t:

The value of the stress concentration factor is calculated by:

where the coefficients in the equation above are calculated from "Peterson's Stress Concentration Factors":

	0.1 ≤ h/r ≤ 2.0	2.0 ≤ h/r ≤ 50.0
C₁	1.024 + 2.092 √h/r − 0.051 (h/r)	1.113 + 1.957 √h/r
C₂	−0.630 − 7.194 √h/r + 1.288 (h/r)	−2.579 − 4.017 √h/r − 0.013 (h/r)
C₃	2.117 + 8.574 √h/r − 2.160 (h/r)	4.100 + 3.922 √h/r + 0.083 (h/r)
C₄	−1.420 − 3.494 √h/r + 0.932 (h/r)	−1.528 − 1.893 √h/r − 0.066 (h/r)

Sources:

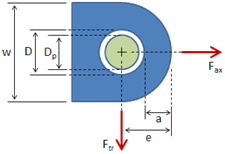
Rectangular Bar With Fillet, Axial Force

This tab defines the stress concentration factor for a bar with a rectangular cross section and a fillet. The bar has an applied axial force (tensile or compressive).

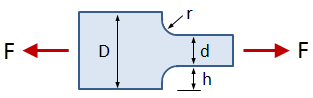
D = width of larger section
d = width of smaller section
r = radius of fillet
t = bar thickness
F = applied force (tensile or compressive)

The maximum stress is calculated as σ_max = K_t σ_nom, where K_t is the stress concentration factor as determined from the plot below, and σ_nom is calculated as:

Input Geometry:

Results:

r/d:

D/d:

h/r:

K_t:

The value of the stress concentration factor is calculated by:

where the coefficients in the equation above are calculated from "Roark's Formulas for Stress and Strain":

	0.1 ≤ h/r ≤ 2.0	2.0 ≤ h/r ≤ 20.0
C₁	1.007 + 1.000 √h/r − 0.031 (h/r)	1.042 + 0.982 √h/r − 0.036 (h/r)
C₂	−0.114 − 0.585 √h/r + 0.314 (h/r)	−0.074 − 0.156 √h/r − 0.010 (h/r)
C₃	0.241 − 0.992 √h/r − 0.271 (h/r)	−3.418 + 1.220 √h/r − 0.005 (h/r)
C₄	−0.134 + 0.577 √h/r − 0.012 (h/r)	3.450 − 2.046 √h/r + 0.051 (h/r)

Sources:

Rectangular Bar With Fillet, Bending

This tab defines the stress concentration factor for a bar with a rectangular cross section and a fillet. The bar has an applied in-plane bending moment.

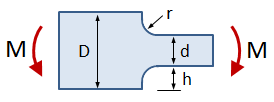
D = width of larger section
d = width of smaller section
r = radius of fillet
t = bar thickness
M = applied bending moment

The maximum stress is calculated as σ_max = K_t σ_nom, where K_t is the stress concentration factor as determined from the plot below, and σ_nom is calculated as:

Input Geometry:

Results:

r/d:

D/d:

h/r:

K_t:

The value of the stress concentration factor is calculated by:

where the coefficients in the equation above are calculated from "Roark's Formulas for Stress and Strain":

	0.1 ≤ h/r ≤ 2.0	2.0 ≤ h/r ≤ 20.0
C₁	1.007 + 1.000 √h/r − 0.031 (h/r)	1.042 + 0.982 √h/r − 0.036 (h/r)
C₂	−0.270 − 2.404 √h/r + 0.749 (h/r)	−3.599 + 1.619 √h/r − 0.431 (h/r)
C₃	0.677 + 1.133 √h/r − 0.904 (h/r)	6.084 − 5.607 √h/r + 1.158 (h/r)
C₄	−0.414 + 0.271 √h/r + 0.186 (h/r)	−2.527 + 3.006 √h/r − 0.691 (h/r)

Sources:

Need More Functionality?

Sign up for an account to receive full access to all calculators and other content. The subscription types are described below, along with the benefits of each.