Column Buckling
Short compression members will fail once the stress exceeds the compressive yield strength of the material. However, long compression members will fail due to buckling before the yield strength of the member is reached. Buckling occurs suddenly, and is characterized by large deflections perpendicular to the axis of the column.
A simple way to demonstrate column buckling is to hold a ruler at either end and to push your hands toward one another. The ruler will buckle at the center.
Contents
Columns with Central Loading
Columns with loads applied along the central axis are either analyzed using the Euler formula for "long" columns, or using the Johnson formula for "intermediate" columns.
Euler Formula for Long Columns
The Euler column formula can be used to analyze for buckling of a long column with a load applied along the central axis:
In the equation above, σcr is the critical stress (the average stress at which the column will buckle), and Pcr is the critical force (the applied force at which the column will buckle). A is the cross sectional area, L is the unsupported length of the column, r is the radius of gyration of the cross section, and E is the elastic modulus of the material. K is the effective length factor, and accounts for the end conditions of the column. The effective length factor is discussed in more detail in the following section.
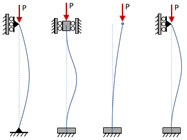
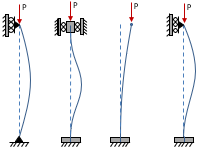
Column End Conditions
The value of the effective length factor, K, is dependent on the end conditions of the column, as shown in the table below:
| End Condition: | Pinned-Pinned | Fixed-Fixed | Fixed-Pinned | Fixed-Free |
| Illustration: |

|

|

|
|
| Theoretical Effective Length Factor, K: | 1 | 0.5 | 0.699 | 2 |
| Recommended Effective Length Factor, K: | 1 | 0.9 | 0.9 | 2.1 |
| NOTE : Table adapted from Gere and Lindeburg. To be conservative, the maximum recommended values were used. | ||||
The effective length factor is used as a means of relating columns with differing end conditions. The effective length of a column is the length of an equivalent pinned-pinned column, and is calculated as:
where Leff is the effective length and L is the actual unsupported length of the column. For example, the theoretical effective length of a fixed-free column is 2L. The fixed-free column is twice as susceptible to buckling as a pinned-pinned column, such that the fixed-free column is effectively twice as long as a pinned-pinned column with the same material and geometry (and so will buckle under half the load). Another way to think about is is that for the two columns to buckle under the same load, the pinned-pinned column would have to be twice as long as the fixed-free column.
Need a Column Buckling Calculator?
Try our column buckling calculator.
- buckling analysis of long and intermediate-length columns loaded in compression
- loading can be either central or eccentric
An alternative to the effective length factor, K, is the end coefficient, C. The end coefficient and the effective length factor are related by:
The theoretical values for the C factor are:
| End Condition: | Pinned-Pinned | Fixed-Fixed | Fixed-Pinned | Fixed-Free |
| Theoretical End Coefficient, C: | 1 | 4 | 2 | 0.25 |
The effective length factor, K, and the end coefficient, C, are both common in the literature. A table is given at the end of this page which summarizes the column buckling formulas using both the K factor and the C factor.
Slenderness Ratio
In the Euler column formula, the quantity L/r is referred to as the slenderness ratio:
The slenderness ratio indicates the susceptibility of the column to buckling. Columns with a high slenderness ratio are more susceptible to buckling and are classified as "long" columns. Long columns are analyzed with the Euler formula. Columns with a lower slenderness ratio are classified as "intermediate" columns and are analyzed with the Johnson formula.
The transition slenderness ratio can be calculated for a column which indicates the cutoff between long and intermediate columns. The transition slenderness ratio is the value of the slenderness ratio at which the Euler critical stress, σcr, is equal to half the material yield strength, Sy: (Note 1)
Columns with a slenderness ratio less than the transition slenderness ratio are considered intermediate columns.
Johnson Formula for Intermediate Columns
The Euler formula is valid for predicting buckling failures for long columns under a centrally applied load. However, for shorter ("intermediate") columns the Euler formula will predict very high values of critical force that do not reflect the failure load seen in practice. To account for this, a correction curve is used for intermediate columns. The Johnson formula (or "Johnson parabola") has been shown to correlate well with actual column buckling failures, and is given by the equation below: (Note 1)
Euler Formula vs Johnson Formula
The plot below shows the Euler curve for a pinned-pinned column with a 1 inch diameter circular cross section and a material of 6061-T6 Aluminum:
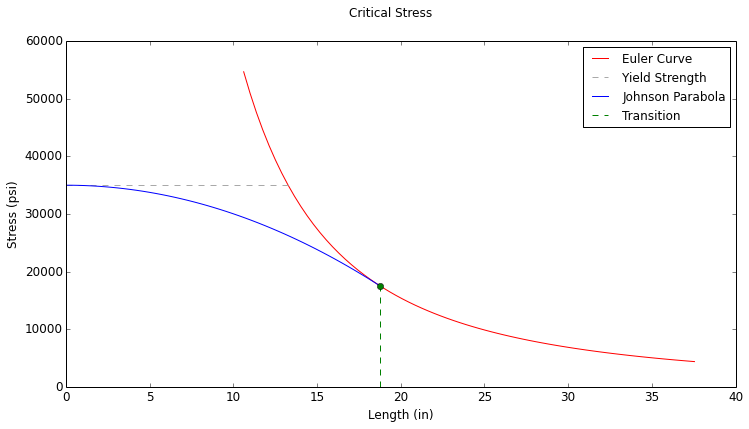
Note the Euler curve shown in red in the plot above. As column length approaches zero, the Euler critical stress approaches infinity. The Johnson formula is shown as the blue curve, and it corrects for the unrealistically high critical stresses predicted by the Euler curve for shorter columns.
Need a Column Buckling Calculator?
Try our column buckling calculator.
- buckling analysis of long and intermediate-length columns loaded in compression
- loading can be either central or eccentric
Columns with Eccentric Loading
In practice, loads are commonly applied at an offset from the central axis. These eccentric loads can be the result of design, or the result of deviations introduced during manufacture or assembly.
The eccentricity ratio relates the eccentricity of the load to the cross section dimensions:
where e is the eccentricity, c is the centroidal distance, and r is the radius of gyration. According to Gere, values of eccentricity ratio are most commonly less than 1, but typical values are between 0 to 3. Imperfections in a centrally loaded column are commonly approximated by using an eccentricity ratio of 0.25.
The maximum deflection in the column can be found by:
The maximum compressive stress in the column can be found by:
The compressive stress calculated above accounts for the axial stress as well as the bending stress due to the moment. The moment arm is a combination of both the eccentricity and the maximum deflection in the column.
The critical force is the value of the applied force, P, at which the maximum compressive stress in the column equals the compressive yield strength of the material. This value of critical force is denoted Pcrit. The equation for maximum compressive stress cannot be solved directly for Pcrit, and so the solution must be found iteratively.
Note that the equation for maximum compressive stress is a function of the average stress, P/A, and so the value Pcrit/A is the value of the average stress at which the maximum compressive stress in the column equals the material yield strength:
Since sources will vary in which formulation is used, it should be noted that the following are equivalent:
The secant formula used for eccentric columns is only valid for pinned-pinned or fixed-free columns. The differential equation used to derive the secant formula does not apply to a fixed-pinned column. For a fixed-fixed column, the concept of an eccentrically applied load has no meaning since the effect of the eccentricity is to induce a moment at the ends of the beam, and any moment at the ends of the beam would be resisted by the fixed supports and would not induce any bending in the column.
Summary of Equations
Because of the prevalence in literature of both the effective length factor, K, and the end coefficient, C, a table summarizing the column buckling equations using both factors is given below. The equations using K are shown in the left column, and the equations using C are shown in the right column.
Columns with Central Loading
| Using Effective Length Factor, K | Using End Coefficient, C | |
|---|---|---|
| Euler Equation: |
|
|
| Johnson Formula: |
|
|
| Transition Slenderness Ratio: |
|
|
Columns with Eccentric Loading
| Using Effective Length Factor, K | Using End Coefficient, C | |
|---|---|---|
| Max Deflection: |
|
|
| Max Compressive Stress: |
|
|
PDH Classroom offers a continuing education course based on this column buckling reference page. This course can be used to fulfill PDH credit requirements for maintaining your PE license.
Now that you've read this reference page, earn credit for it!
Notes
Note 1: Yield Strength
The relevant yield strength for column buckling problems is the compressive yield strength. For ductile materials, compressive strength is approximately equal to tensile strength. For brittle materials, compressive strength is higher than tensile strength. If compressive strength is not known, it can be conservatively assumed that compressive strength is equal to tensile strength.
References
- Budynas-Nisbett, "Shigley's Mechanical Engineering Design," 8th Ed.
- Gere, James M., "Mechanics of Materials," 6th Ed.
- Hibbeler, Russell C., "Mechanics of Materials," 10th Ed.
- Lindeburg, Michael R., "Mechanical Engineering Reference Manual for the PE Exam," 13th Ed.
- "Stress Analysis Manual," Air Force Flight Dynamics Laboratory, October 1986.