The table below gives properties of common cross sections. More extensive tables can be found in the listed references.

The properties calculated in the table include area, centroidal moment of inertia, section modulus, and radius of gyration. For information on cross section properties, see our on cross section properties reference.

Shape	Representation	Properties
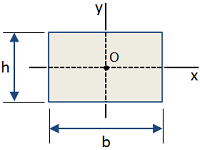
Rectangle		Area [in2]: A = bh Moment of Inertia [in4]: Section Modulus [in3]: Radius of Gyration [in]:
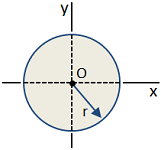
Circle		Area [in2]: Moment of Inertia [in4]: Section Modulus [in3]: Radius of Gyration [in]:
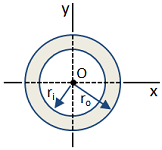
Circular Tube		Area [in2]: Moment of Inertia [in4]: Section Modulus [in3]: Radius of Gyration [in]:
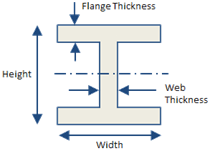
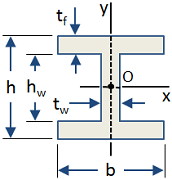
I-Beam		Area [in2]: Moment of Inertia [in4]: Section Modulus [in3]:

---

---

References

1. Gere, James M., "Mechanics of Materials," 6th Ed.
2. Lindeburg, Michael R., "Mechanical Engineering Reference Manual for the PE Exam," 13th Ed.

---

---