Column Buckling Calculator

Check out our column buckling calculator based on the methodology described here.

Column Buckling Calculator

Column Buckling Validation

Calculator
Instructions Reference Validation
Column Buckling Calculator

This section details the validation for the Column Buckling calculator. Several examples are worked through to determine expected results such as critical stress, critical force, and critical length. These expected results are then compared to the actual output of the Column Buckling calculator.

Case 1 Case 2 Case 3

Case 3: Eccentric Load, Pinned-Pinned

In this validation, a column with the following properties will be analyzed:

Applied Compressive Load, F: 5000 lbf
Material: 6061-T6 Aluminum
Yield Strength, Sty = 35,000 psi
Elastic Modulus, E = 10e6 psi
Cross Section: Circle, 1 inch diameter
Area, A = 0.7854 in2
Centroidal Distance, c = 0.5 in
Radius of Gyration, r = 0.25 in
Length (unsupported), L: 24 in
Eccentricity: 0.035 in
End Condition: Pinned-Pinned (K = 1)
Pinned-Pinned Column

Manual Calculations

This case is the exact same as Case 1 with the only exception being that the load is applied with a slight eccentricity. The amount of eccentricity that is applied in this case is on the order of that which might be expected due to imperfections.

The slenderness ratio of this column is:

$$ R_s = {L \over r} = {24 \text{ in} \over 0.25 \text{ in}} = 96.0 $$

The eccentricity ratio of this column is:

$$ R_{e} = { ec \over r^2 } = { (0.035 \text{ in})(0.5 \text{ in}) \over (0.25 \text{ in})^2 } = 0.28 $$

The maximum compressive stress in the column can be found by:

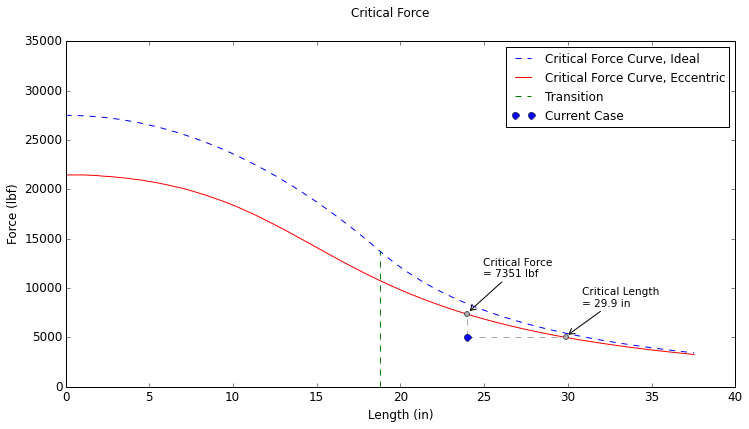
$$ \sigma_{c,max} = {P \over A} \left[ 1 + { ec \over r^2 } \sec\left( {KL \over 2r } \sqrt{ {P \over AE} } \right) \right] $$

The critical force is found by iterating the value of \(P\) in the equation above until the maximum compressive stress equals the compressive yield strength of the material. At a force of \(P = 7351 \text{ lbf}\), the maximum compressive stress in the column is:

$$\begin{eqnarray} \sigma_{c,max} &=& {P \over A} \left[ 1 + { ec \over r^2 } \sec\left( {KL \over 2r } \sqrt{ {P \over AE} } \right) \right] \nonumber \\ &=& {7351 \text{ lbf} \over 0.7854 \text{ in}^2} \left[ 1 + { (0.035 \text{ in})(0.5 \text{ in}) \over (0.25 \text{ in})^2 } \sec\left( {(1)(24 \text{ in}) \over 2(0.25 \text{ in}) } \sqrt{ {7351 \text{ lbf} \over (0.7854 \text{ in}^2)(10e6 \text{ psi})} } \right) \right] \nonumber \\ &=& 35,019 \text{ psi} \end{eqnarray}$$

Since \(35,019 \text{ psi} \) is almost exactly equal to the yield strength of the material, it can be concluded that the value \(P = 7351 \text{ lbf}\) is the critical force which will cause buckling of the column.

Comparison With Calculator

The critical force calculated above matches the value in the Critical Force Plot below:

Critical Force