Bolted Joint Analysis Validation
This section details the validation for the Bolted Joint calculator. Several examples are worked through to determine expected results such as joint constant, joint separation, bolt forces and stresses, and clamped part stresses. These expected results are then compared to the actual output of the Bolted Joint Analysis calculator.
Case 3: Tapped Joint, 2 Plates
In this validation, a bolted joint with the following properties will be analyzed:
| Applied Forces: |
Tensile Force, Ftens = 300 lbf Shear Force, Fsh = 0 lbf |
| Materials: |
316 SS (Elastic Mod, E = 28e6 psi, Yield Str, Sty = 30 ksi) ASTM A572 (Elastic Mod, E = 30e6 psi, Yield Str, Sty = 50 ksi) |
| Joint Properties: | Type = Tapped Joint Preload = 0.67*[Yield Strength] |
| Bolt Properties: |
Thread Size = 1/4"-20 (Anom = 0.0491 in2, At = 0.0318 in2) Material = 316 SS |
| Clamped Parts: |
Washer: 316 SS, t = 0.065 in Plate: ASTM A572, t = 0.5 in Plate: 316 SS, t = 0.5 in |
Manual Calculations
The grip length, Lg is the total thickness of the parts within the grip. Since this is a tapped joint, the effective grip thickness of the tapped plate must be calculated:
$$ L_{g.p2}^{'} = { \min (t_{p2}, d_{nom}) \over 2} = { \min (0.5 \text{in}, 0.25 \text{in}) \over 2} = 0.125 \text{ in} $$The grip thickness is the total thickness of all parts in the grip, accounting for the effective grip thickness of the tapped plate:
$$ L_g = \sum L_p = 0.065 \text{ in} + 0.5 \text{ in} + 0.125 \text{ in} = 0.69 \text{ in} $$The length (lead) of a single thread is the pitch, \(P\). For a 1/4"-20 bolt, the pitch is:
$$ P = {1 \over TPI} = {1 \over 20 \text{ in}^{-1} } = 0.05 \text{ in} $$The bolt should be sized such that there is at least 1 diameter of thread engagement, or if the plate is not thick enough to allow this the bolt should protrude beyond the plate. An additional 2 threads of length should also be added to the bolt.
$$ L_{b.min} = L_g + L_{g.p2}^{'} + 2P = 0.69 \text{ in} + 0.125 \text{ in} + 2(0.05 \text{ in}) = 0.915 \text{ in} $$Rounding up to the nearest standard length, the bolt length is:
$$ L_b = 1.0 \text{ in} $$An image is provided to the right which shows all of the different lengths that are added up to give the total bolt length. Note that the grip length of the tapped plate is actually counted twice. The reason for this is that we want the bolt thread engagement to be at least \( \min(t_{p2}, d_{nom}) \). Since the grip length of the tapped plate is half of this value, we count it twice to ensure the desired thread engagement.
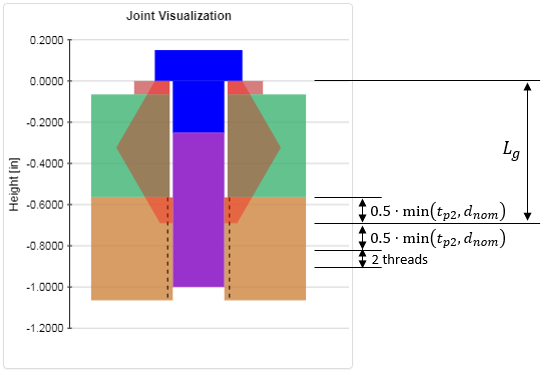
The thread length is calculated per ASME B18.2.1. The thread and shank lengths of the bolt are:
| Thread length: | $$ L_{thd} = 2 d_{nom} + {1 \over 4} \text{ in} = 0.75 \text{ in} $$ |
| Shank length: | $$ L_{shank} = L_b - L_{thd} = 1.0 \text{ in} - 0.75 \text{ in} = 0.25 \text{ in} $$ |
| Thread length in the grip: | $$ L_{thd.g} = L_g - L_{shank} = 0.69 \text{ in} - 0.25 \text{ in} = 0.44 \text{ in} $$ |
The bolt stiffness is calculated based on the stiffness of the shank and the threads in the grip:
| Stiffness of shank: | $$ k_{shank} = {A_{nom} E_{bolt} \over L_{shank} } = {(0.0491 \text{ in}^2) (28e6 \text{ psi}) \over 0.25 \text{ in} } = 5,497,787 \text{ lbf/in} $$ |
| Stiffness of threads in grip: | $$ k_{thd} = {A_t E_{bolt} \over L_{thd.g} } = {(0.0318 \text{ in}^2) (28e6 \text{ psi}) \over 0.44 \text{ in} } = 2,024,968 \text{ lbf/in} $$ |
Bolt Stiffness: |
$$\begin{eqnarray} k_{bolt} &=& {1 \over 1/k_{shank} + 1/k_{thd}} \nonumber \\ &=& {1 \over 1/(5,497,787 \text{ lbf/in}) + 1/(2,024,968 \text{ lbf/in})} \nonumber \\ &=& 1,479,889 \text{ lbf/in} \end{eqnarray}$$ |
A reasonable approximation of the grip stiffness can be obtained by first calculating an effective elastic modulus for the grip:
$$ E_{eff} = { \sum E_p L_p \over \sum L_p } = { (28e6 \text{ psi})(0.065 \text{ in}) + (30e6 \text{ psi})(0.5 \text{ in}) + (30e6 \text{ psi})(0.125 \text{ in}) \over 0.69 \text{ in} } = 29.81e6 \text{ psi} $$The approximate grip stiffness can now be calculated as:
$$ k_{grip} = {\pi E d_{nom} \tan\alpha \over 2 \ln \left[ 5 { (L_g \tan\alpha + 0.5 d_{nom}) \over (L_g \tan\alpha + 2.5 d_{nom}) } \right] } = {\pi (29.81e6 \text{ psi}) (0.25 \text{ in}) \tan(30^{\circ}) \over 2 \ln \left[ 5 { (0.69 \text{ in}) \tan(30^{\circ}) + 0.5 (0.25 \text{ in}) \over (0.69 \text{ in}) \tan(30^{\circ}) + 2.5 (0.25 \text{ in}) } \right] } = 7,199,099 \text{ lbf/in} $$The joint constant is calculated as:
$$ C = { k_{bolt} \over k_{bolt} + k_{grip} } = { 1,479,889 \text{ lbf/in} \over 1,479,889 \text{ lbf/in} + 7,199,099 \text{ lbf/in} } = 0.171 $$The value of the joint constant calculated above is based on an approximate grip stiffness, so it will be an approximate value as well.
The preload force is calculated as:
$$ F_{PL} = P_{pct} S_{ty} A_t = 0.67 (30,000 \text{ psi}) (0.0318 \text{ in}^2) = 640 \text{ lbf} $$The joint separation force is calculated as:
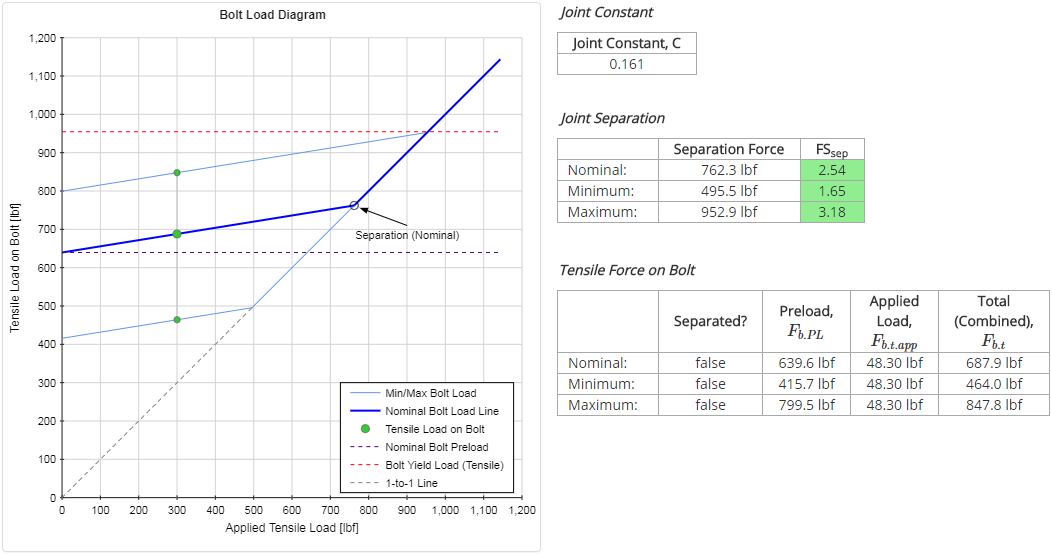
$$ F_{sep} = { F_{PL} \over 1 - C } = { 640 \text{ lbf} \over 1 - 0.171 } = 771 \text{ lbf} $$Since the applied tensile force is less than the separation force, the joint is not separated.
The tensile forces on the bolt are calculated as:
| Bolt tension due to preload: | $$ F_{b.PL} = F_{PL} = 640 \text{ lbf} $$ |
| Bolt tension due to applied load: | $$ F_{b.t.app} = C F_{t.app} = 0.171 (300 \text{ lbf}) = 51 \text{ lbf} $$ |
| Total (combined) tensile force on bolt: | $$ F_{b.t} = F_{b.PL} + F_{b.t.app} = 640 \text{ lbf} + 51 \text{ lbf} = 691 \text{ lbf} $$ |
Comparison With Calculator
The results for this case as output from the Bolted Joint Analysis calculator are shown below. Because the joint constant determined in the manual calculations was approximate, all of the results calculated using that joint constant will also be approximate. With that in mind, the manual calculations are all very close to the results output below.