Bolted Joint Analysis Validation
This section details the validation for the Bolted Joint calculator. Several examples are worked through to determine expected results such as joint constant, joint separation, bolt forces and stresses, and clamped part stresses. These expected results are then compared to the actual output of the Bolted Joint Analysis calculator.
Case 1: Bolt With Nut, 2 Plates
In this validation, a bolted joint with the following properties will be analyzed:
| Applied Forces: |
Tensile Force, Ftens = 500 lbf Shear Force, Fsh = 0 lbf |
| Materials: |
316 SS (Elastic Mod, E = 28e6 psi, Yield Str, Sty = 30 ksi) ASTM A572 (Elastic Mod, E = 30e6 psi, Yield Str, Sty = 50 ksi) |
| Joint Properties: | Type = Bolt With Nut Preload = 0.67*[Yield Strength] |
| Bolt Properties: |
Thread Size = 1/4"-20 (Anom = 0.0491 in2, At = 0.0318 in2) Material = 316 SS |
| Clamped Parts: |
Washer: 316 SS, t = 0.065 in Plate: ASTM A572, t = 0.4 in Plate: ASTM A572, t = 0.5 in Washer: 316 SS, t = 0.065 in |
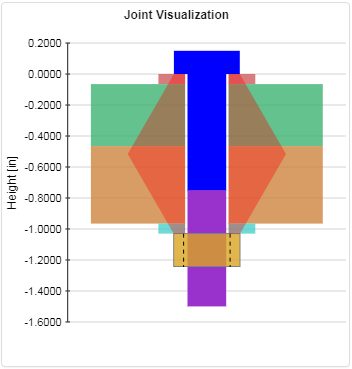
Manual Calculations
The grip length, Lg is the total thickness of the parts within the grip. In this case, there are 2 washers and 2 plates in the grip:
$$ L_g = \sum L_p = 2(0.065 \text{ in}) + 0.4 \text{ in} + 0.5 \text{ in} = 1.03 \text{ in} $$The nut thickness can be determined based on the tables of standard hardware dimensions. The height of a 1/4" hex nut is 0.212 inches.
The length (lead) of a single thread is the pitch, \(P\). For a 1/4"-20 bolt, the pitch is:
$$ P = {1 \over TPI} = {1 \over 20 \text{ in}^{-1} } = 0.05 \text{ in} $$The end of the bolt should protrude past the nut by at least 2 threads. The minimum bolt length is calculated as:
$$ L_{b.min} = L_g + H_n + 2P = 1.03 \text{ in} + 0.212 \text{ in} + 2(0.05 \text{ in}) = 1.342 \text{ in} $$Rounding up to the nearest standard length, the bolt length is:
$$ L_b = 1.5 \text{ in} $$The thread length is calculated per ASME B18.2.1. The thread and shank lengths of the bolt are:
| Thread length: | $$ L_{thd} = 2 d_{nom} + {1 \over 4} \text{ in} = 0.75 \text{ in} $$ |
| Shank length: | $$ L_{shank} = L_b - L_{thd} = 1.5 \text{ in} - 0.75 \text{ in} = 0.75 \text{ in} $$ |
| Thread length in the grip: | $$ L_{thd.g} = L_g - L_{shank} = 1.03 \text{ in} - 0.75 \text{ in} = 0.28 \text{ in} $$ |
The bolt stiffness is calculated based on the stiffness of the shank and the threads in the grip:
| Stiffness of shank: | $$ k_{shank} = {A_{nom} E_{bolt} \over L_{shank} } = {(0.0491 \text{ in}^2) (28e6 \text{ psi}) \over 0.75 \text{ in} } = 1,832,596 \text{ lbf/in} $$ |
| Stiffness of threads in grip: | $$ k_{thd} = {A_t E_{bolt} \over L_{thd.g} } = {(0.0318 \text{ in}^2) (28e6 \text{ psi}) \over 0.28 \text{ in} } = 3,182,092 \text{ lbf/in} $$ |
Bolt Stiffness: |
$$\begin{eqnarray} k_{bolt} &=& {1 \over 1/k_{shank} + 1/k_{thd}} \nonumber \\ &=& {1 \over 1/(1,832,596 \text{ lbf/in}) + 1/(3,182,092 \text{ lbf/in})} \nonumber \\ &=& 1,162,882 \text{ lbf/in} \end{eqnarray}$$ |
A reasonable approximation of the grip stiffness can be obtained by first calculating an effective elastic modulus for the grip:
$$ E_{eff} = { \sum E_p L_p \over \sum L_p } = { 2(28e6 \text{ psi})(0.065 \text{ in}) + (30e6 \text{ psi})(0.4 \text{ in}) + (30e6 \text{ psi})(0.5 \text{ in}) \over 1.03 \text{ in} } = 29.75e6 \text{ psi} $$The approximate grip stiffness can now be calculated as:
$$ k_{grip} = {\pi E d_{nom} \tan\alpha \over 2 \ln \left[ 5 { (L_g \tan\alpha + 0.5 d_{nom}) \over (L_g \tan\alpha + 2.5 d_{nom}) } \right] } = {\pi (29.75e6 \text{ psi}) (0.25 \text{ in}) \tan(30^{\circ}) \over 2 \ln \left[ 5 { (1.03 \text{ in}) \tan(30^{\circ}) + 0.5 (0.25 \text{ in}) \over (1.03 \text{ in}) \tan(30^{\circ}) + 2.5 (0.25 \text{ in}) } \right] } = 6,233,981 \text{ lbf/in} $$The joint constant is calculated as:
$$ C = { k_{bolt} \over k_{bolt} + k_{grip} } = { 1,162,882 \text{ lbf/in} \over 1,162,882 \text{ lbf/in} + 6,233,981 \text{ lbf/in} } = 0.157 $$The value of the joint constant calculated above is based on an approximate grip stiffness, so it will be an approximate value as well.
The preload force is calculated as:
$$ F_{PL} = P_{pct} S_{ty} A_t = 0.67 (30,000 \text{ psi}) (0.0318 \text{ in}^2) = 640 \text{ lbf} $$The joint separation force is calculated as:
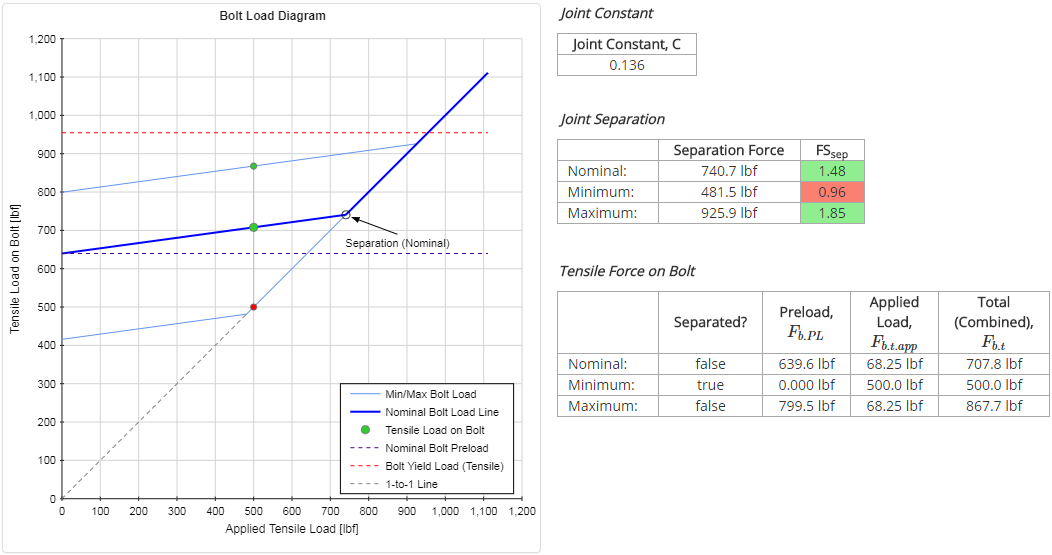
$$ F_{sep} = { F_{PL} \over 1 - C } = { 640 \text{ lbf} \over 1 - 0.157 } = 759 \text{ lbf} $$Since the applied tensile force is less than the separation force, the joint is not separated.
The tensile forces on the bolt are calculated as:
| Bolt tension due to preload: | $$ F_{b.PL} = F_{PL} = 640 \text{ lbf} $$ |
| Bolt tension due to applied load: | $$ F_{b.t.app} = C F_{t.app} = 0.157 (500 \text{ lbf}) = 79 \text{ lbf} $$ |
| Total (combined) tensile force on bolt: | $$ F_{b.t} = F_{b.PL} + F_{b.t.app} = 640 \text{ lbf} + 79 \text{ lbf} = 718 \text{ lbf} $$ |
Comparison With Calculator
The results for this case as output from the Bolted Joint Analysis calculator are shown below. Because the joint constant determined in the manual calculations was approximate, all of the results calculated using that joint constant will also be approximate. With that in mind, the manual calculations are all very close to the results output below.
It should be noted that for the minimum value of preload, which is based on preload uncertainty due to installation and preload relaxation, the joint separates. This is considered a failure and the joint should be redesigned to avoid separation.