Beam Analysis Validation
This section details the validation for the Beam calculator. Several examples are worked through to determine expected results such as deflections, forces, and stresses. These expected results are then compared to the actual output of the calculator.
Cantilever Beam, Uniform Distributed Force
The standard beam equations for a cantilever beam loaded with a uniform distributed force are given below:
| Max Deflection: | $$ \delta_{max} = {w L^4 \over 8EI} $$ | @ x = L |
| Max Slope: | $$ \theta_{max} = {w L^3 \over 6EI} $$ | @ x = L |
| Max Shear: | $$ V_{max} = +wL $$ | @ x = 0 |
| Max Moment: | $$ M_{max} = -{w L^2 \over 2 } $$ | @ x = 0 |
For the validation case, an Aluminum 6061-T6 beam with a 1 inch diameter circular cross-section and a length of 10 inches will be loaded with a uniform distributed force of 100 lbf/in. Since the beam is 10 inches long, the total force applied to the beam is 1000 lbf. The inputs are:
For the given inputs, the expected results are:
| Max Deflection: | \( \delta_{max} = 0.2572 \text{ in} \) | @ x = L |
| Max Slope: | \( \theta_{max} = 0.03430 \text{ rad} \) | @ x = L |
| Max Shear: | \( V_{max} = +1000 \text{ lbf} \) | @ x = 0 |
| Max Moment: | \( M_{max} = -5000 \text{ in-lbf} \) | @ x = 0 |
Comparison With Calculator
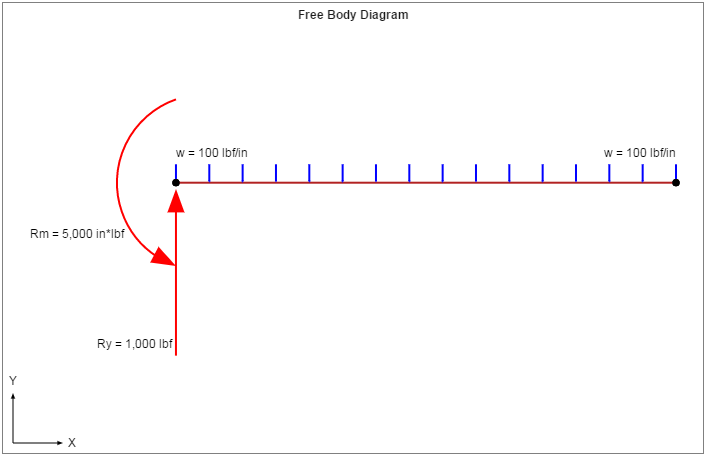
Free Body Diagram
The Free Body Diagram (FBD) is shown below. From the FBD it can be seen that the forces balance and the beam is in static equilibrium.
Deflection & Slope
A screenshot of the results table giving the maximum deflection and slope is shown below. While the results aren't an exact match to the expected values, the error is minimal. The error on maximum deflection is 0.66% (0.2589 in versus the ideal 0.2572 in), and the error on maximum slope is 0.79% (0.03464 rad versus the ideal 0.03430 rad). The reason for the error is that the beam analysis is solved as a finite element model, and distributed forces are applied to the beam by applying a force to each node (as opposed to an ideal continuum).
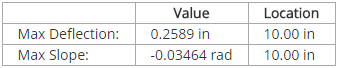
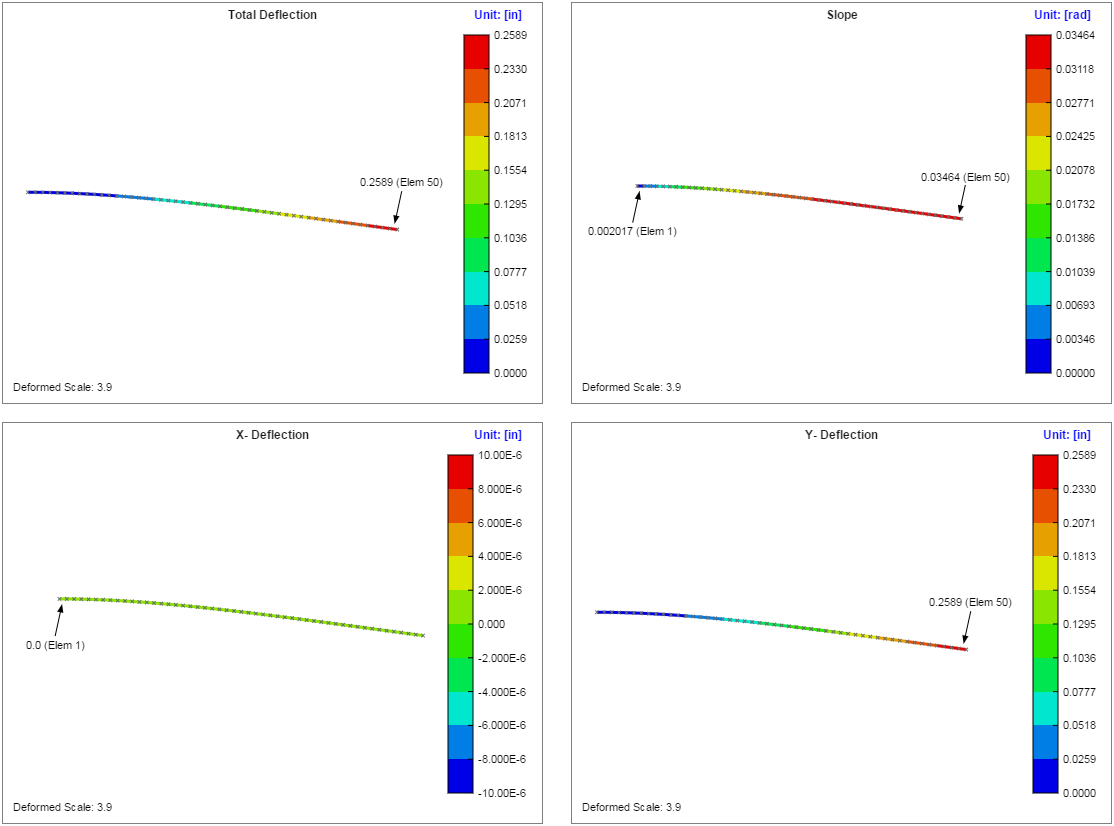
The deflection plots are shown below. From these plots it can be seen that a maximum deflection of 0.2589 inches occurs at the free end of the beam as well as a maximum slope of 0.03464 radians.
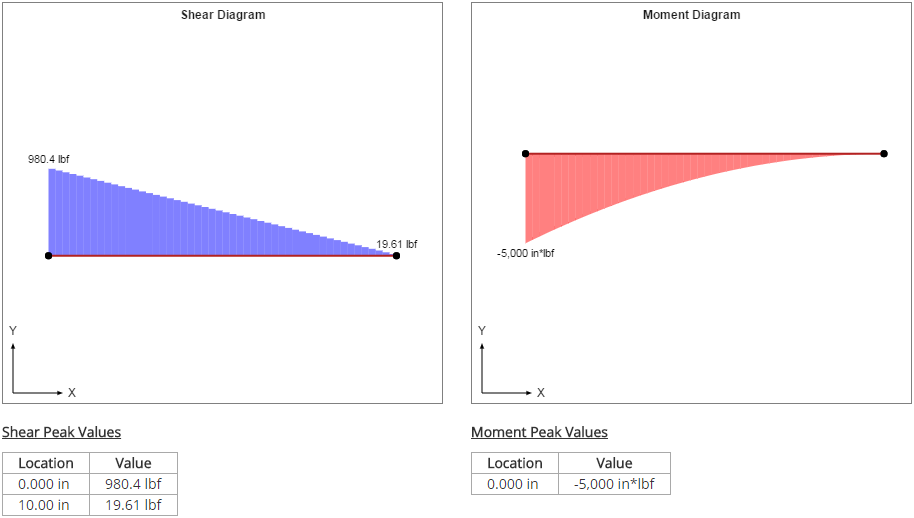
Shear-Moment Diagram
The shear-moment diagram for the beam is shown below. In the ideal case, the peak shear force at x = 0 would be 1000 lbf and the peak moment at x = 0 would be 5000 in-lbf. However, since the distributed force is applied as concentrated loads on discrete nodes (rather than as an ideal continuum), there is some error in the results. In this case, the peak shear force at x = 0 is reported as 980.4 lbf rather than 1000 lbf.
The overall trends of the shear and moment diagrams are what would be expected. The shear force decreases linearly from the fixed end of the beam to the free end. The magnitude of the moment decreases parabolically from the fixed end of the beam to the free end.
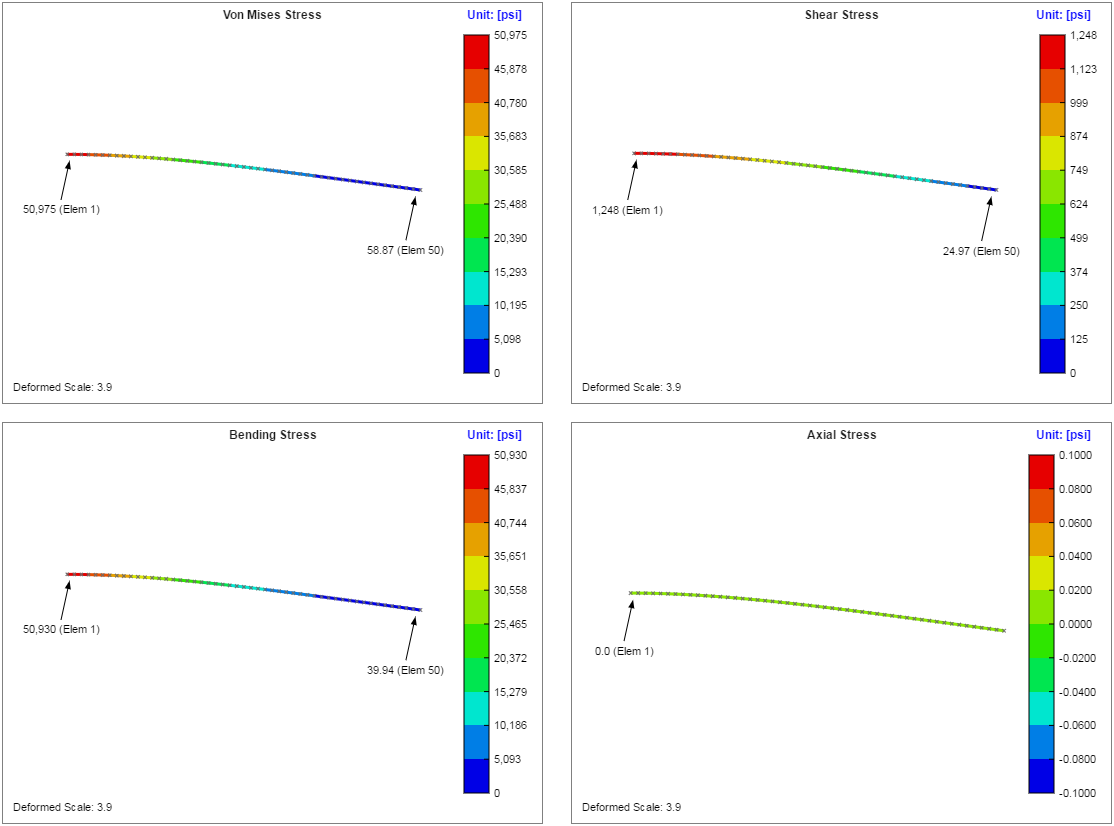
Stresses
The stresses will be validated at the fixed end of the beam. At this point, the ideal forces are:
| Axial (lbf) | Shear (lbf) | Moment (in-lbf) | |
|---|---|---|---|
| Forces @ x = 0: | $$ F_{ax} = 0 $$ | $$ F_{sh} = 1000 $$ | $$ M = 5000 $$ |
The stresses are calculated using the following equations:
| Axial Stress | Shear Stress | Bending Stress | Von Mises Stress |
|---|---|---|---|
| $$ \sigma_{ax} = {F_{ax} \over A} $$ | $$ \tau_{sh} = {F_{sh} \over A} $$ | $$ \sigma_{b} = {Mc \over I} $$ | $$ \sigma_{vm} = \sqrt{ (\sigma_{ax} + \sigma_{b})^2 + 3\tau_{sh}^2 } $$ |
Based on the equations above, the ideal and calculated stresses at the fixed end are:
| Axial, \( \sigma_{ax} \) (psi) | Shear, \( \tau_{sh} \) (psi) | Bending, \( \sigma_{b} \) (psi) | Von Mises, \( \sigma_{vm} \) (psi) | |
|---|---|---|---|---|
| Ideal: | $$ 0 $$ | $$ 1273 $$ | $$ 50930 $$ | $$ 50977 $$ |
| Calculated: | $$ 0 \text{ (0.00% error)} $$ | $$ 1248 \text{ (1.96% error)} $$ | $$ 50930 \text{ (0.00% error)} $$ | $$ 50975 \text{ (0.00% error)} $$ |
The stress plots are shown below: